题目内容
【题目】如图,四棱柱ABCD-![]() 中,地面ABCD为直角梯形,AB∥CD,AB⊥BC,平面ABCD⊥平面AB
中,地面ABCD为直角梯形,AB∥CD,AB⊥BC,平面ABCD⊥平面AB![]() ,∠BA
,∠BA![]() =60°,AB=A
=60°,AB=A![]() =2BC=2CD=2
=2BC=2CD=2
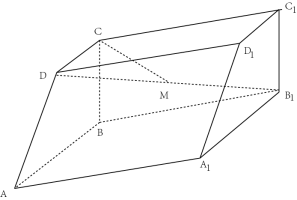
(1)求证:BC⊥A![]() ;
;
(2)求二面角D-A![]() -B的余弦值;
-B的余弦值;
(3)在线段D![]() 上是否存在点M,使得CM∥平面DA
上是否存在点M,使得CM∥平面DA![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)证明![]() 平面
平面![]() 得到答案.
得到答案.
(2)![]() 为
为![]() 中点,
中点,![]() 于
于![]() ,连接
,连接![]() ,
,![]() 为二面角D-A
为二面角D-A![]() -B的平面角,计算得到答案.
-B的平面角,计算得到答案.
(3)存在,![]() 为
为![]() 中点,连接
中点,连接![]() ,
,![]() ,证明平面
,证明平面![]() 平面
平面![]() ,得到答案.
,得到答案.
(1)平面ABCD⊥平面AB![]() ,AB⊥BC,故
,AB⊥BC,故![]() 平面
平面![]() ,
,![]() 平面
平面![]()
故![]() .
.
(2)如图所示:![]() 为
为![]() 中点,
中点,![]() 于
于![]() ,连接
,连接![]()
![]() ,
,![]() 为
为![]() 中点,故
中点,故![]() ,
,![]() 为平行四边形,故
为平行四边形,故![]()
故![]() 平面
平面![]() ,
,![]() ,故
,故![]() 为二面角D-A
为二面角D-A![]() -B的平面角.
-B的平面角.
![]() ,
,![]() ,
,![]() ,
,![]()
故二面角D-A![]() -B的余弦值为
-B的余弦值为![]()
(3)存在,![]() 为
为![]() 中点,连接
中点,连接![]() ,
,![]()
则![]() ,
,![]() 为平行四边形,故
为平行四边形,故![]() ,
,![]()
![]() ,
,![]() ,故平面
,故平面![]() 平面
平面![]()
![]() 为
为![]() 中点,
中点,![]() ,故四棱柱
,故四棱柱![]() ,
,![]() 和
和![]() 相交
相交
当![]() 为
为![]() 和
和![]() 交点时,满足
交点时,满足![]() 平面
平面![]() ,故
,故![]() 平面
平面![]()
此时![]() 为
为![]() 中点,故
中点,故![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
X | 1 | 2 | 3 | 4 | 5 |
频率 | a | 0.2 | 0.45 | b | c |
(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为4的3件日用品记为![]() ,等级系数为5的2件日用品记为
,等级系数为5的2件日用品记为![]() ,现从
,现从![]() ,
,![]() 这5件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.
这5件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.
【题目】某高校健康社团为调查本校大学生每周运动的时长,随机选取了80名学生,调查他们每周运动的总时长(单位:小时),按照![]()
![]()
![]()
![]()
![]()
![]() 共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
表1:男生
时长 |
|
|
|
|
|
|
人数 | 2 | 8 | 16 | 8 | 4 | 2 |
表2:女生
时长 |
|
|
|
|
|
|
人数 | 0 | 4 | 12 | 12 | 8 | 4 |
(1)从每周运动时长不小于20小时的男生中随机选取2人,求选到“运动达人”的概率;
(2)根据题目条件,完成下面![]() 列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
每周运动的时长小于15小时 | 每周运动的时长不小于15小时 | 总计 | |
男生 | |||
女生 | |||
总计 | |||
参考公式: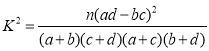 ,其中
,其中![]() .
.
参考数据:
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |