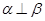题目内容
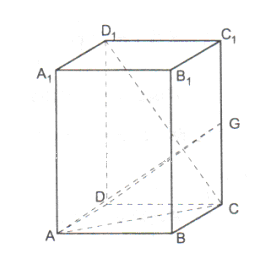
如图,长方体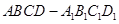 中,
中,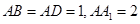 ,G是
,G是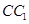 上的动点。
上的动点。
(l)求证:平面ADG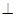
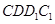 ;
;
(2)判断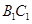 与平面ADG的位置关系,并给出证明;
与平面ADG的位置关系,并给出证明;
(3)若G是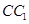 的中点,求二面角G-AD-C的大小;
的中点,求二面角G-AD-C的大小;
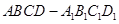 中,
中,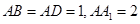 ,G是
,G是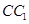 上的动点。
上的动点。(l)求证:平面ADG
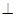
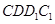 ;
;(2)判断
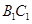 与平面ADG的位置关系,并给出证明;
与平面ADG的位置关系,并给出证明;(3)若G是
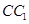 的中点,求二面角G-AD-C的大小;
的中点,求二面角G-AD-C的大小;
(1)详见解析(2)详见解析(3)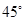
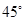
试题分析:(1)在长方体
 中,
中,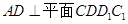 ,且
,且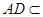 平面
平面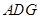 ,
,可得平面
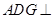 平面
平面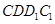
(2)由
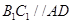 ,且
,且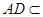 平面
平面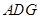 ,
, 平面
平面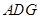 可知
可知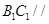 平面
平面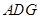
(3)首先由
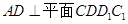 证明
证明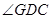 是二面角
是二面角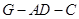 的平面角,再利用等腰直角三角形
的平面角,再利用等腰直角三角形
求出
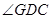 的大小.
的大小.试题解析:(1)
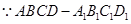 是长方体,且
是长方体,且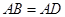
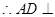 平面
平面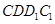
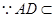 平面
平面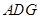 , 平面
, 平面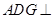 平面
平面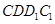
(2)当点
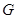 与
与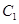 重合时,
重合时,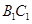 在平面
在平面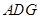 内,
内,当点
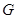 与
与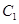 不重合时,
不重合时,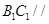 平面
平面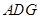
证明:
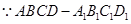 是长方体,
是长方体,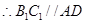
若点
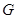 与
与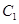 重合,平面
重合,平面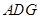 即
即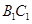 与
与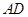 确定的平面,
确定的平面,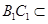 平面
平面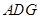
若点
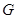 与
与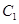 不重合
不重合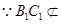 平面
平面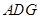 ,
,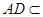 平面
平面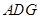 且
且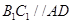
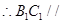 平面
平面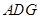
(3)
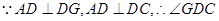 为二面角
为二面角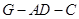 的平面角
的平面角在
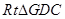 中,
中,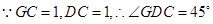

练习册系列答案
相关题目
 ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.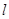 ,求证:
,求证:
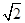 EF.
EF.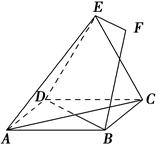
 AB.Q是PC上的一点.
AB.Q是PC上的一点.
 是两条不同直线,
是两条不同直线, 是两个不同平面,下列四个命题中正确的是( )
是两个不同平面,下列四个命题中正确的是( ) 所成的角相等,则
所成的角相等,则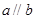
 ,
, ,
, ,则
,则 ,
, ,
, ,则
,则
 ,
, ,
, 是两条不重合的直线,
是两条不重合的直线, 是三个不重合的平面,则
是三个不重合的平面,则 的一个充分条件是( )
的一个充分条件是( )



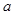 ,b,c是空间三条不同的直线,
,b,c是空间三条不同的直线,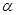 ,
,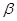 是空间两个不同的平面,则下列命题不成立的是( )
是空间两个不同的平面,则下列命题不成立的是( )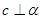 时,若
时,若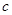 ⊥
⊥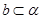 ,且
,且