题目内容
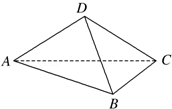
在几何体ABCDE中,∠BAC= ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
(1)设平面ABE与平面ACD的交线为直线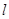 ,求证:
,求证: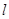 ∥平面BCDE;
∥平面BCDE;
(2)设F是BC的中点,求证:平面AFD⊥平面AFE;
(3)求几何体ABCDE的体积.

 ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.(1)设平面ABE与平面ACD的交线为直线
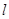 ,求证:
,求证: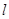 ∥平面BCDE;
∥平面BCDE;(2)设F是BC的中点,求证:平面AFD⊥平面AFE;
(3)求几何体ABCDE的体积.

(1)详见解析;(2)详见解析;(3)2.
试题分析:(1)根据两条直线同垂直于一个平面,这两条直线平行可得DC//EB,再有直线与平面平行的判定定理得出直线DC∥平面ABE,由于
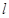 是平面ABE与平面ACD的交线,可得DC∥
是平面ABE与平面ACD的交线,可得DC∥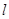 ,又由直线与平面平行的判定定理
,又由直线与平面平行的判定定理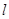 ∥平面BCDE.(2)先证AF⊥平面BCDE,再证FD⊥平面AFE,最后证明平面AFD⊥平面AFE.(3)由等体积公式求解,即
∥平面BCDE.(2)先证AF⊥平面BCDE,再证FD⊥平面AFE,最后证明平面AFD⊥平面AFE.(3)由等体积公式求解,即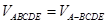 .
.【证】(1)∵DC⊥平面ABC,EB⊥平面ABC,
∴DC//EB,又∵DC
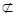 平面ABE,EB
平面ABE,EB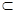 平面ABE,
平面ABE,∴DC∥平面ABE,
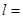 平面ABE
平面ABE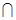 平面ACD,则DC∥
平面ACD,则DC∥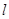 ,
,又
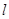
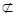 平面BCDE,CD
平面BCDE,CD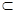 平面BCDE,
平面BCDE,所以
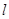 ∥平面BCDE.(4分)
∥平面BCDE.(4分)【解】(2)在△DEF中,
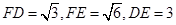 ,由勾股定理知,
,由勾股定理知,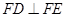
由DC⊥平面ABC,AF
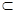 平面ABC,∴DC⊥AF,
平面ABC,∴DC⊥AF,又∵AB=AC,F是BC的中点,∴AF⊥BC,
又∵DC∩BC=C,DC
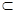 平面BCDE ,BC
平面BCDE ,BC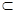 平面BCDE,
平面BCDE,∴AF⊥平面BCDE,∴AF⊥FD,又∵AF∩FE=F,∴FD⊥平面AFE,
又FD
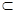 平面AFD,故平面AFD⊥平面AFE.(9分)
平面AFD,故平面AFD⊥平面AFE.(9分)(3)
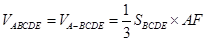 =
=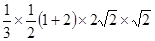 =2.(13分)
=2.(13分)
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
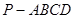 的底面为菱形,
的底面为菱形,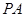
 面
面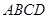 ,且
,且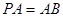 ,
,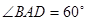 ,
,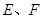 分别是
分别是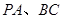 的中点.
的中点.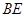 ∥平面
∥平面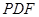 ;
;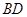 作一平面交棱
作一平面交棱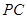 于点
于点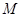 ,若二面角
,若二面角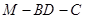 的大小为
的大小为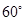 ,求
,求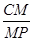 的值.
的值.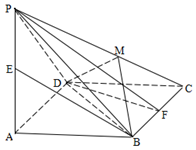
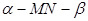 的大小为
的大小为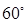 ,菱形
,菱形 在面
在面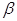 内,
内,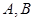 两点在棱
两点在棱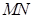 上,
上,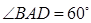 ,
,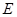 是
是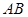 的中点,
的中点,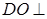 面
面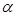 ,垂足为
,垂足为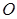 .
.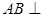 平面
平面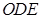 ;
;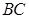 与
与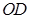 所成角的余弦值.
所成角的余弦值.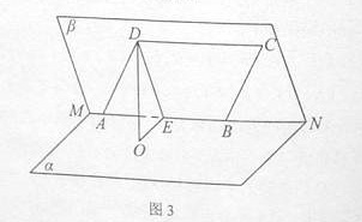
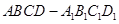 中,
中,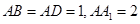 ,G是
,G是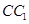 上的动点。
上的动点。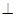
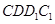 ;
;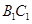 与平面ADG的位置关系,并给出证明;
与平面ADG的位置关系,并给出证明;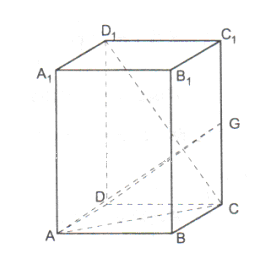
 、
、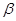 和直线
和直线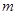 ,给出条件:①
,给出条件:①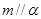 ;②
;②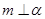 ;③
;③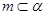 ;④
;④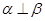 ;⑤
;⑤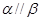 .
.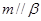 的是( )
的是( )