题目内容
【题目】若定义在R上的偶函数f(x)满足f(x﹣1)=f(x+1).且当x∈[﹣1,0]时,f(x)=﹣x2+1,如果函数g(x)=f(x)﹣a|x|恰有8个零点,则实数a的值为 .
【答案】8﹣2 ![]()
【解析】解:由f(x+1)=f(x﹣1),则f(x)=f(x﹣2),故函数f(x)为周期为2的周期函数.
∵函数g(x)=f(x)﹣a|x|恰有8个零点,
∴f(x)﹣a|x|=0在(﹣∞,0)上有四个解,
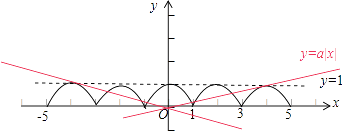
即f(x)的图象(图中黑色部分)与直线y=a|x|(图中红色直线)在(﹣∞,0)上有4个交点,
如图所示:
又当x∈[﹣1,0]时,f(x)=﹣x2+1,
∴当直线y=﹣ax与y=﹣(x+4)2+1相切时,即可在(﹣∞,0)上有4个交点,
∴x2+(8﹣a)x+15=0,∴△=(8﹣a)2﹣60=0.
∵a>0,∴a=8﹣2 ![]() .
.
所以答案是:8﹣2 ![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目