题目内容
已知函数![]() ,且当
,且当![]() 时,
时,![]() 的最小值为2.(1)求
的最小值为2.(1)求![]() 的值,并求
的值,并求![]() 的单调增区间;(2)将函数
的单调增区间;(2)将函数![]() 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的![]() 倍,再把所得图象向右平移
倍,再把所得图象向右平移![]() 个单位,得到函数
个单位,得到函数![]() ,求方程
,求方程![]() 在区间
在区间![]() 上的所有根之和.
上的所有根之和.
解析: (1)![]() ……2分.
……2分.
∵![]() ∴
∴![]()
![]() ,故
,故![]() ,
, ![]()
由![]() ,解得
,解得![]() ,
, ![]()
故![]() 的单调增区间是
的单调增区间是![]() ,
,![]()
(2)![]()
由![]() 得
得![]() ,则
,则![]() 或
或![]()
解得![]() 或
或![]() ,
,![]() ;
;
∵![]() ∴
∴![]() 或
或![]()
故方程所有根之和为![]() .
.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
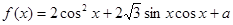 ,且当
,且当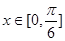 时,
时,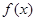 的最小值为2.
的最小值为2.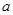 的值,并求
的值,并求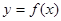 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的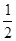 倍,再把所得图象向右平移
倍,再把所得图象向右平移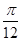 个单位,得到函数
个单位,得到函数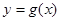 ,求方程
,求方程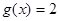 在区间
在区间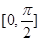 上的所有根之和.
上的所有根之和.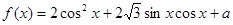 ,且当
,且当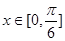 时,
时,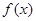 的最小值为2.
的最小值为2.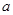 的值,并求
的值,并求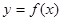 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的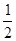 ,再把所得图象向右平移
,再把所得图象向右平移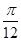 个单位,得到函数
个单位,得到函数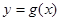 ,求方程
,求方程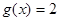 在区间
在区间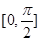 上的所有根之和.
上的所有根之和.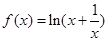 ,且
,且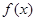 在
在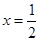 处的切线方程为
处的切线方程为 .
.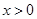 时,恒有
时,恒有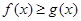 ;
;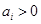 ,
,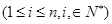 ,且
,且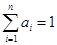 ,则
,则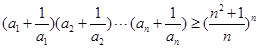 .
.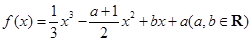 ,且其导函数
,且其导函数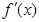 的图像过原点.
的图像过原点.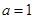 时,求函数
时,求函数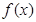 的图像在
的图像在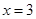 处的切线方程;
处的切线方程;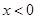 ,使得
,使得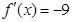 ,求
,求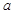 的最大值;
的最大值;