题目内容
已知函数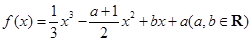 ,且其导函数
,且其导函数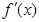 的图像过原点.
的图像过原点.
(1)当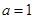 时,求函数
时,求函数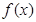 的图像在
的图像在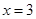 处的切线方程;
处的切线方程;
(2)若存在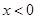 ,使得
,使得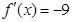 ,求
,求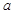 的最大值;
的最大值;
【答案】
(1) 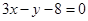 (2)-7
(2)-7
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)根据导数的计算,以及导函数过原点,且在a=1的情况下,分析得到结论。
(2)对于参数a进行讨论,分析要是导函数在-9时,方程有解。,对于a分为几种情况分别说明,a>0,a<0,a=0。
解: 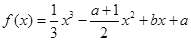 ,
,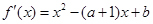
由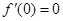 得
得 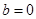 ,
,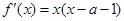 . ---------------------2分
. ---------------------2分
(1) 当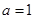 时,
时, 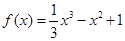 ,
,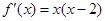 ,
,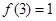 ,
,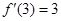
所以函数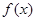 的图像在
的图像在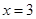 处的切线方程为
处的切线方程为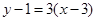 ,即
,即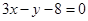 ------------4分
------------4分
(2) 存在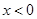 ,使得
,使得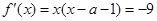 ,
,
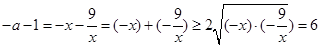 ,
,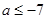 ,
,
当且仅当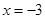 时,
时, 所以
所以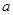 的最大值为
的最大值为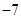 .
-----------------9分
.
-----------------9分

练习册系列答案
相关题目
 x2,g(x)=logax(a>0且a≠1),
x2,g(x)=logax(a>0且a≠1),