题目内容
已知函数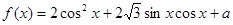 ,且当
,且当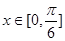 时,
时,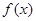 的最小值为2.
的最小值为2.
(1)求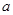 的值,并求
的值,并求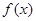 的单调增区间;
的单调增区间;
(2)将函数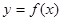 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的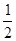 ,再把所得图象向右平移
,再把所得图象向右平移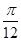 个单位,得到函数
个单位,得到函数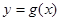 ,求方程
,求方程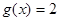 在区间
在区间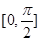 上的所有根之和.
上的所有根之和.
【答案】
(1) ,
,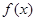 的单调增区间是
的单调增区间是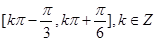 ;(2)
;(2) .
.
【解析】
试题分析:(1)首先应用三角函数的倍角公式及辅助角公式,将原三角函数式化简成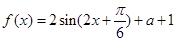 ,关键其在
,关键其在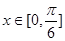 的最值,建立
的最值,建立 的方程;
的方程;
由 解得
解得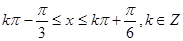 ,得到
,得到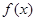 的单调增区间是
的单调增区间是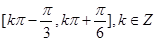 .
.
(2)遵循三角函数图象的变换规则,得到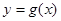 ,利用特殊角的三角函数值,解出方程
,利用特殊角的三角函数值,解出方程 在区间
在区间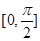 上的所有根,求和。
上的所有根,求和。
试题解析:(1)
∵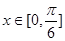 ∴
∴
 ,故
,故 ,
,
由 ,解得
,解得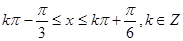
故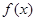 的单调增区间是
的单调增区间是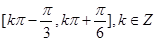
(2)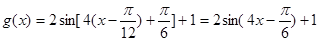
由 得
得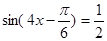 ,则
,则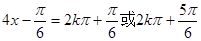
解得 ;
;
∵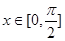 ∴
∴ ,故方程所有根之和为
,故方程所有根之和为 .
.
考点:三角函数的和差倍半公式,三角函数图象的变换.

练习册系列答案
相关题目
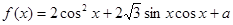 ,且当
,且当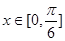 时,
时,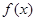 的最小值为2.
的最小值为2.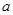 的值,并求
的值,并求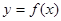 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的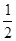 倍,再把所得图象向右平移
倍,再把所得图象向右平移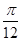 个单位,得到函数
个单位,得到函数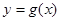 ,求方程
,求方程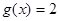 在区间
在区间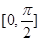 上的所有根之和.
上的所有根之和.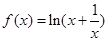 ,且
,且 在
在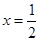 处的切线方程为
处的切线方程为 .
.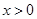 时,恒有
时,恒有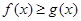 ;
;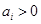 ,
,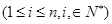 ,且
,且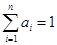 ,则
,则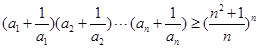 .
.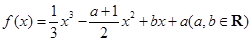 ,且其导函数
,且其导函数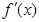 的图像过原点.
的图像过原点.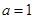 时,求函数
时,求函数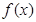 的图像在
的图像在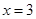 处的切线方程;
处的切线方程;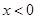 ,使得
,使得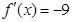 ,求
,求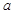 的最大值;
的最大值;