题目内容
已知三点A（cosα,sinα）、B（cosβ,sinβ）、C(cosγ,sinγ).若向量
+k
+(2-k)
=0(k为常数，且0＜k＜2
,求cos(β-γ)的最大值、最小值及相应的k值.
解析：由已知得
移项得
⑴2+⑵2得k2+(2-k)2+2k(2-k)cos(β-γ)=1.
∴cos(β-γ)=-=1+
=1+
.
∵0＜k＜2,故k=1时，cos(β-γ)有最大值-
.
又cos(β-γ)≥-1，故cos(β-γ)的最小值为-1.
此时1+
=-1，解得k=
或k=
.
综上所述，当k=1时，cos(β-γ)有最大值-
，当k=
或k=
时，cos(β-γ)有最小值-1.
练习册系列答案
相关题目
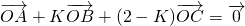（k为常数且0＜k＜2，O为坐标原点，S△BOC表示△BOC的面积）
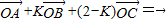（k为常数且0＜k＜2，O为坐标原点，S△BOC表示△BOC的面积）