题目内容
已知三点A(cosα,sinα),B(cosβ,sinβ),C(cosγ,sinγ),若向量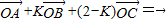 (k为常数且0<k<2,O为坐标原点,S△BOC表示△BOC的面积)
(k为常数且0<k<2,O为坐标原点,S△BOC表示△BOC的面积)(1)求cos(β-γ)的最值及相应的k的值;
(2)求cos(β-γ)取得最大值时,S△BOC:S△AOC:S△AOB.
【答案】分析:(1)将已知中的向量关系变形为等式的一边有一个向量,将等式平方求出cos(β-γ)的函数式,分离常数,利用二次函数的最值求出范围
(2)将k值代入向量等式求出三个向量的夹角,又三个向量的模相等,得到三个三角形全等,得到三角形的面积比.
解答:解:(1)由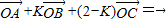 得
得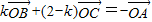
两边平方,得k2+(2-k)2+2k(2-k)cos(β-γ)=1
整理得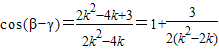
当k∈(0,2)时,k2-2k∈[-1,0),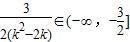 ,
,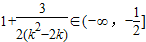
又cos(β-γ)∈[-1,1],
∴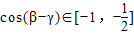
当k=1时,cos(β-γ)取得最大值 ;
;
当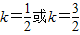 时,cos(β-γ)取得最小值-1.
时,cos(β-γ)取得最小值-1.
(2)由(1)得,cos(β-γ)取得最大值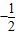 时,k=1
时,k=1
此时,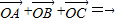 且
且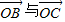 的夹角为120°.
的夹角为120°.
又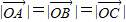 ,
,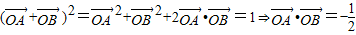
∴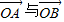 的夹角为120°.
的夹角为120°.
故S△BOC:S△AOC:S△AOB=1:1:1.
点评:本题考查向量的运算法则、两角和的公式、分离常数求二次函数的值域、利用向量的数量积求出向量的夹角.
(2)将k值代入向量等式求出三个向量的夹角,又三个向量的模相等,得到三个三角形全等,得到三角形的面积比.
解答:解:(1)由
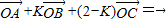 得
得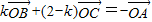
两边平方,得k2+(2-k)2+2k(2-k)cos(β-γ)=1
整理得
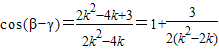
当k∈(0,2)时,k2-2k∈[-1,0),
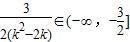 ,
,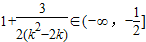
又cos(β-γ)∈[-1,1],
∴
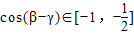
当k=1时,cos(β-γ)取得最大值
 ;
;当
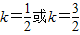 时,cos(β-γ)取得最小值-1.
时,cos(β-γ)取得最小值-1.(2)由(1)得,cos(β-γ)取得最大值
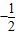 时,k=1
时,k=1此时,
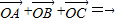 且
且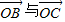 的夹角为120°.
的夹角为120°.又
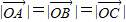 ,
,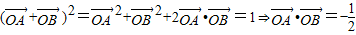
∴
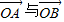 的夹角为120°.
的夹角为120°.故S△BOC:S△AOC:S△AOB=1:1:1.
点评:本题考查向量的运算法则、两角和的公式、分离常数求二次函数的值域、利用向量的数量积求出向量的夹角.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
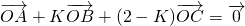 (k为常数且0<k<2,O为坐标原点,S△BOC表示△BOC的面积)
(k为常数且0<k<2,O为坐标原点,S△BOC表示△BOC的面积)