题目内容
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=BC=BB1 , AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD. 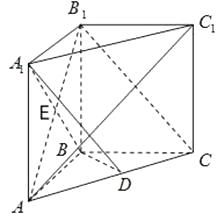
(1)求证:BD⊥平面A1ACC1;
(2)若AB=1,且ACAD=1,求二面角B﹣A1D﹣B1的余弦值.
【答案】
(1)证明:连结ED,
∵平面AB1C∩平面A1BD=ED,B1C∥平面A1BD,
∴B1C∥ED,
∵E为AB1中点,∴D为AC中点,
∵AB=BC,∴BD⊥AC①,
法一:由A1A⊥平面ABC,BD平面ABC,得A1A⊥BD,②,
由①②及A1A、AC是平面A1ACC1内的两条相交直线,
得BD⊥平面A1ACC1.
法二:由A1A⊥平面ABC,A1A平面A1ACC1,
∴平面A1ACC1⊥平面ABC,又平面A1ACC1∩平面ABC=AC,
得BD⊥平面A1ACC1.
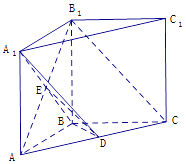
(2)解:由AB=1,得BC=BB1=1,
由(1)知DA= ![]() AC,又ACDA=1,得AC2=2,
AC,又ACDA=1,得AC2=2,
∵AC2=2=AB2+BC2,∴AB⊥BC,
如图以B为原点,建立空间直角坐标系B﹣xyz,如图示,
则A1(1,0,1),B1(0,0,1),D( ![]() ),
),
得 ![]() =(1,0,0),
=(1,0,0), ![]() =(
=( ![]() ),
),
设 ![]() =(x,y,z)是平面A1B1D的一个法向量,
=(x,y,z)是平面A1B1D的一个法向量,
则 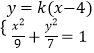 ,令z=1,得
,令z=1,得 ![]() =(0,2,1),
=(0,2,1),
设 ![]() =(a,b,c)为平面A1BD的一个法向量,则
=(a,b,c)为平面A1BD的一个法向量,则 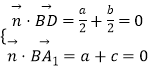 ,
,
令c=1,得 ![]() =(﹣1,1,1),
=(﹣1,1,1),
依题意知二面角B﹣A1D﹣B1为锐二面角,设其大小为θ,
则cosθ=|cos< ![]() >|=
>|= ![]() =
= ![]() =
= ![]() ,
,
即二面角B﹣A1D﹣B1的余弦值为 ![]() .
.
其它解法请参照给分.

【解析】(Ⅰ)法一:连结ED,推导出B1C∥ED,BD⊥AC,A1A⊥BD,由此能证明BD⊥平面A1ACC1 . 法二:连结ED,推导出A1A⊥平面ABC,由平面A1ACC1⊥平面ABC,能证明BD⊥平面A1ACC1 . (Ⅱ)以B为原点,建立空间直角坐标系B﹣xyz,利用向量法能求出二面角B﹣A1D﹣B1的余弦值.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

【题目】[选修4-5:不等式选讲]
已知函数f(x)=|2x﹣a|+a.
(1)当a=3时,求不等式f(x)≤6的解集;
(2)设函数g(x)=|2x﹣3|,x∈R,f(x)+g(x)≥5,求a的取值范围.
