题目内容
函数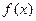 的定义域为
的定义域为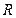 ,并满足条件
,并满足条件
①对任意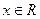 ,有
,有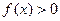 ;
;
②对任意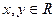 ,有
,有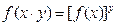 ;
;
③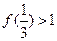 .
.
(1)求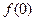 的值;
的值;
 (2)求证:
(2)求证: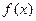 在
在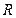 上是单调递增函数;
上是单调递增函数;
(3)若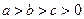 ,且
,且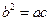 ,求证
,求证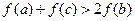 .
.
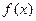 的定义域为
的定义域为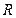 ,并满足条件
,并满足条件①对任意
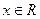 ,有
,有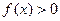 ;
;②对任意
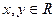 ,有
,有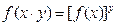 ;
;③
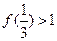 .
.(1)求
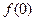 的值;
的值; (2)求证:
(2)求证: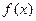 在
在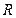 上是单调递增函数;
上是单调递增函数;(3)若
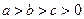 ,且
,且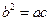 ,求证
,求证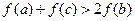 .
.1
解法一:(1)令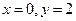 ,则
,则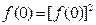
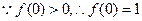
(2)任取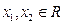 ,且
,且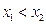
设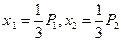 ,则
,则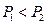
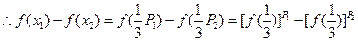
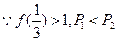 ,
,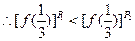
 ,
,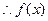 在
在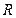 上是单调递增函数
上是单调递增函数
(3)由(1)(2)知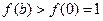 ,
,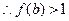
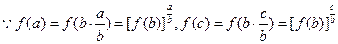
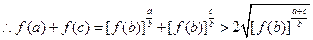
又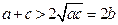 ,
,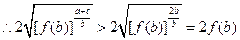

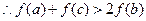
解法二:(1)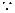 对任意
对任意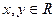 ,有
,有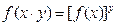
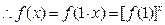
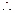 当
当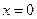 时,
时,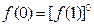
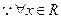 ,
,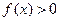 ,
,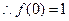
(2)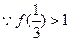 ,
,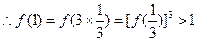
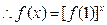 是
是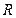 上的单调增函数
上的单调增函数
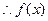 在
在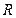 上是单调递增函数
上是单调递增函数
(3)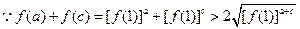
而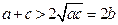 ,
,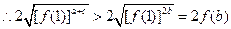
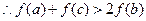
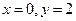 ,则
,则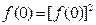
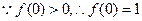
(2)任取
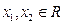 ,且
,且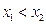
设
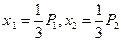 ,则
,则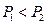
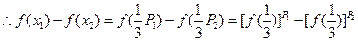
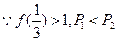 ,
,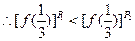
 ,
,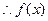 在
在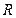 上是单调递增函数
上是单调递增函数 (3)由(1)(2)知
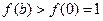 ,
,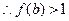
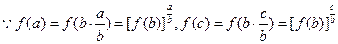
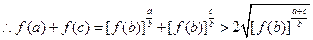
又
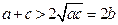 ,
,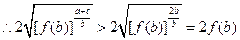

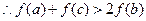
解法二:(1)
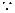 对任意
对任意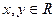 ,有
,有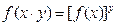
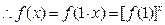
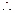 当
当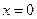 时,
时,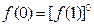
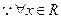 ,
,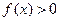 ,
,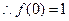
(2)
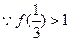 ,
,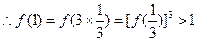
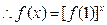 是
是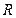 上的单调增函数
上的单调增函数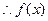 在
在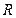 上是单调递增函数
上是单调递增函数 (3)
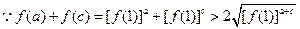
而
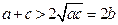 ,
,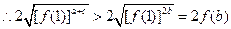

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
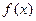 满足:对任意的
满足:对任意的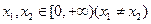 ,有
,有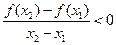 ,则( )
,则( )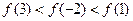
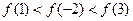
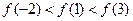
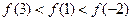
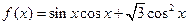
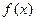 的最小正周期;
的最小正周期;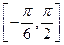 上的最大值和最小值
上的最大值和最小值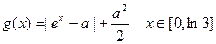 ,求函数
,求函数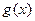 的最小值
的最小值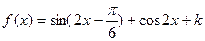
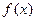 的单调递增区间;
的单调递增区间;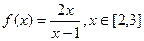 的最大值和最小值。
的最大值和最小值。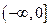 上是单调增函数,若
上是单调增函数,若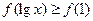 ,则实数x的取值范围是_______________
,则实数x的取值范围是_______________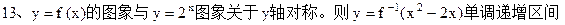 为( )
为( )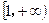 B
B 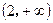 C
C 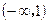 D
D