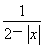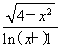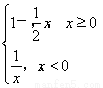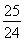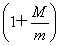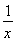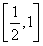题目内容
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数f(x)=1+a·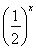 +
+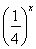 .
.
(1)当a=1时,求函数f(x)在(-∞,0)上的值域,并判断函数f(x)在(-∞,0)上是否为有界函数,请说明理由;
(2)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围.
(1)不是有界函数(2)[-5,1]
【解析】(1)当a=1时,f(x)=1+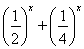
因为f(x)在(-∞,0)上递减,所以f(x)>f(0)=3,即f(x)在(-∞,0)的值域为(3,+∞),
故不存在常数M>0,使|f(x)|≤M成立,
所以函数f(x)在(-∞,0)上不是有界函数.
(2)由题意知,|f(x)|≤3在[0,+∞)上恒成立.
-3≤f(x)≤3,-4-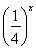 ≤a·
≤a·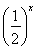 ≤2-
≤2-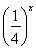 ,所以-4·2x-
,所以-4·2x-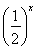 ≤a≤2·2x-
≤a≤2·2x-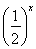 在[0,+∞)上恒成立.所以
在[0,+∞)上恒成立.所以 ≤a≤
≤a≤ ,
,
设2x=t,h(t)=-4t-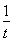 ,p(t)=2t-
,p(t)=2t-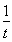 ,由x∈[0,+∞)得t≥1,设1≤t1<t2,h(t1)-h(t2)=
,由x∈[0,+∞)得t≥1,设1≤t1<t2,h(t1)-h(t2)=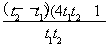 >0,p(t1)-p(t2)=
>0,p(t1)-p(t2)=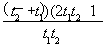 <0,所以h(t)在[1,+∞)上递减,p(t)在[1,+∞)上递增,h(t)在[1,+∞)上的最大值为h(1)=-5,p(t)在[1,+∞)上的最小值为p(1)=1,所以实数a的取值范围为[-5,1].
<0,所以h(t)在[1,+∞)上递减,p(t)在[1,+∞)上递增,h(t)在[1,+∞)上的最大值为h(1)=-5,p(t)在[1,+∞)上的最小值为p(1)=1,所以实数a的取值范围为[-5,1].

练习册系列答案
相关题目