题目内容
17.为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:已知在全部50人中随机抽取1人,抽到喜爱打篮球的学生的概率为$\frac{3}{5}$.(1)请将列联表补充完整(不用写计算过程);
| 喜爱 | 不喜爱 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
(2)若从该班不喜爱打篮球的男生中随机抽取3人调查,求其中某男生甲被选到的概率.
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率,做出喜爱打篮球的人数,进而做出男生的人数,填好表格;根据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看出有多大的把握说明打篮球和性别有关系.
(2)从该班不喜爱打篮球的男生中随机抽取3人调查,共有${C}_{5}^{3}$=10种,某男生甲被选到共有${C}_{4}^{2}$=6种,即可求出概率.
解答 解:(1)列联表补充如下:
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
∴在犯错误的概率不超过0.005的前提下,认为喜爱打篮球与性别有关.
(2)从该班不喜爱打篮球的男生中随机抽取3人调查,共有${C}_{5}^{3}$=10种,某男生甲被选到共有${C}_{4}^{2}$=6种,
∴其中某男生甲被选到的概率是$\frac{6}{10}$=$\frac{3}{5}$.
点评 本题是一个统计综合题,包含独立性检验和概率,本题通过创设情境激发学生学习数学的情感,帮助培养其严谨治学的态度.

练习册系列答案
相关题目
5.在等差数列{an}中,已知a5+a7=8,则该数列前11项和S11=( )
| A. | 44 | B. | 55 | C. | 143 | D. | 176 |
9.已知命题$p:?x∈[{1,2}],\frac{1}{2}{x^2}-lnx-a≥0$是真命题,则实数a的取值范围是( )
| A. | $[{\frac{1}{2},+∞})$ | B. | $({-∞,\frac{1}{2}}]$ | C. | [2-ln2,+∞) | D. | (-∞,2-ln2] |
7.函数f(x)=$\left\{\begin{array}{l}{sinx,x∈(-π,0]}\\{cosx,x∈(0,π)}\end{array}\right.$,则f(-$\frac{π}{3}$)+f($\frac{π}{6}$)+f($\frac{5π}{6}$)+f(-$\frac{2π}{3}$)=( )
| A. | -1 | B. | -$\sqrt{3}$ | C. | -2$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{2}$ |
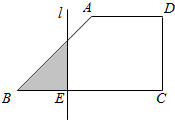 如图,底角∠ABE=45°的直角梯形ABCD,底边BC长为4cm,腰长AB为$2\sqrt{2}$cm,当一条垂直于底边BC的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BE=x,试写出阴影部分的面积y与x的函数关系式,并画出函数大致图象.
如图,底角∠ABE=45°的直角梯形ABCD,底边BC长为4cm,腰长AB为$2\sqrt{2}$cm,当一条垂直于底边BC的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BE=x,试写出阴影部分的面积y与x的函数关系式,并画出函数大致图象.