题目内容
已知平面上直线l的方向向量e=(
),点O（0,0)和A（1，-2）在l上的投影分别是O′和A′，则
=λe，其中λ等于（ ）A.
B.
C.2 D.-2
解析:令e的起点是原点，与e方向相反，排除A、C，设e与夹角为θ.
∵=（1，-2），则||=
，
∴cosθ=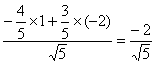
.
∴
在e上的射影|
|·cosθ=
=-2.∴λ=-2.
答案:D
练习册系列答案
相关题目
已知平面上直线l的方向向量
=（-
，
），点O（0，0）和A（1，-2）在l上的射影分别是O'和A′，则
=λ
，其中λ等于（ ）
| e |
| 4 |
| 5 |
| 3 |
| 5 |
| O′A′ |
| e |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
已知平面上直线l的方向向量
=(
，-
)，点O（0，0）和P（-2，2）在直线l的正射影分别是O'和P'，且
=λ
，则λ等于（ ）
| e |
| ||
| 2 |
| 1 |
| 2 |
| O′P′ |
| e |
A、-2(
| ||
B、2(
| ||
C、-(
| ||
D、
|
)，点O(0,0)和A(1,-2)在l上的射影分别是O1、A1，则
=λe，其中λ等于( )
B.
C.2 D.-2