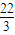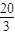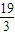题目内容
设椭圆 的右焦点为F,C为椭圆短轴上的端点,向量
的右焦点为F,C为椭圆短轴上的端点,向量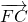 绕F点顺时针旋转90°后得到向量
绕F点顺时针旋转90°后得到向量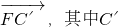 点恰好落在椭圆右准线上,则该椭圆的离心率为________.
点恰好落在椭圆右准线上,则该椭圆的离心率为________.
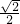
分析:先设出F,C两点坐标,由题意能够得出△CFC'是等腰直角三角形,然后根据焦半径公式得出|FC|=|FC'|=a,再根据右准线为x=
 =
= a,即可求出结果.
a,即可求出结果.解答:设F(c,0),C(0,b)
由题意可知|FC|=|FC'|∠CFC'=90° 所以△CFC'是等腰直角三角形
∴|FC|=|FC'|=a
∵∠CFC'=90°
∴|CC'|=
 a
a∴右准线为x=
 =
= a 即
a 即 =
=
∴离心率e=

故答案为
 .
.点评:本题考查了椭圆的简单性质,根据题意得出△CFC'是等腰直角三角形,是解题的关键,属于基础题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
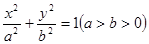 的右焦点为F,C为椭圆短轴的端点,向量
的右焦点为F,C为椭圆短轴的端点,向量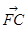 绕F点顺时针旋转
绕F点顺时针旋转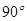 后得到向量
后得到向量 ,其中
,其中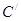 点恰好落在直线
点恰好落在直线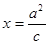 上,则该椭圆的离心率为__________________________
上,则该椭圆的离心率为__________________________ 的右焦点为F,P为椭圆上一动点,A(1,1),则
的右焦点为F,P为椭圆上一动点,A(1,1),则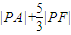 的最小值为( )
的最小值为( )


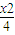 +
+ =1上有n个不同的点P1,P2,P3,…,Pn.设椭圆的右焦点为F,数列{|PnF|}是公差大于
=1上有n个不同的点P1,P2,P3,…,Pn.设椭圆的右焦点为F,数列{|PnF|}是公差大于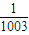 的等差数列,则n的最大值为( )
的等差数列,则n的最大值为( )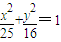 的右焦点为F,P为椭圆上一动点,A(1,1),则
的右焦点为F,P为椭圆上一动点,A(1,1),则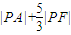 的最小值为( )
的最小值为( )