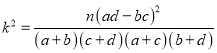Question

【题目】O为原点的直角坐标系中，点A（4，﹣3）为△OAB的直角顶点，已知AB=2OA，且点B的纵坐标大于0
（1）求 的坐标；
（2）求圆C1：x2﹣6x+y2+2y=0关于直线OB对称的圆C2的方程；在直线OB上是否存在点P，过点P的任意一条直线如果和圆C1圆C2都相交，则该直线被两圆截得的线段长相等，如果存在求出点P的坐标，如果不存在，请说明理由．

Answer 1

【答案】
（1）解：设 =（x，y），由AB=2OA， =0

得 ，解得 或

若 ，则yB=﹣11与点B的纵坐标大于0矛盾

若 ，则yB=5符合，即 =（6，8）

（2）解：C1：x2﹣6x+y2+2y=0，即（x﹣3）2+（y+1）2=10，所以C1（3，﹣1），r=

∵ =（10，5），∴直线OB的方程为 x

设C2（a，b），则 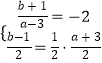，∴a=1，b=3．

所以圆C2的方程为（x﹣1）2+（y﹣3）2=10

存在点P，根据图形的对称性，点P即为线段C1C2的中点，坐标为（2，1）．

【解析】（1）由AB=2OA， =0，点B的纵坐标大于0，求 的坐标；（2）求出圆C2的方程，即可得出结论．