题目内容
△ABC的三个内角A、B、C的对边的长分别为a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)
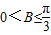 ;
;(2)
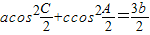 ;
;(3)
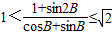 .
.请你选取给定的两个条件中的一个条件为条件,三个结论中的两个为结论,组建一个你认为正确的命题,并证明之.
(I)组建的命题为:已知 ______
求证:①______
②______
(II)证明:
【答案】分析:(1)利用a、b、c成等差数列可推断出2b=a+c,代入关于B的余弦定理中利用基本不等式求得cosB的范围,进而求得B的范围,原式得证.
(2)利用二倍角公式和余弦定理对原式进行化简整理求得等式成立,原式得证.
解答:解:(I)可以组建命题:△ABC中,若a、b、c成等差数列,求证:①0<B≤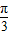
②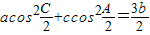 ;
;
(II)①∵a、b、c成等差数列∴2b=a+c,
∴b=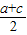
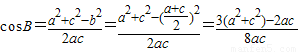 ≥
≥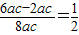
且B∈(0,π),∴0<B≤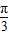
②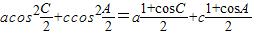 =
=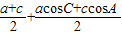 =
=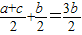
故答案为:a、b、c成等差数列,0<B≤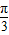 ,
,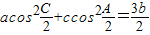 .
.
点评:本题主要考查了数列与三角函数的综合,余弦定理的应用,二倍角的化简求值.考查了学生对基础知识的理解和灵活运用.
(2)利用二倍角公式和余弦定理对原式进行化简整理求得等式成立,原式得证.
解答:解:(I)可以组建命题:△ABC中,若a、b、c成等差数列,求证:①0<B≤
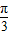
②
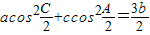 ;
;(II)①∵a、b、c成等差数列∴2b=a+c,
∴b=
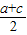
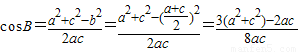 ≥
≥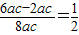
且B∈(0,π),∴0<B≤
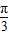
②
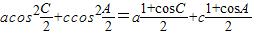 =
=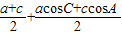 =
=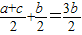
故答案为:a、b、c成等差数列,0<B≤
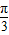 ,
,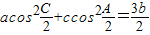 .
.点评:本题主要考查了数列与三角函数的综合,余弦定理的应用,二倍角的化简求值.考查了学生对基础知识的理解和灵活运用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=
,A+C=2B,则sinC=( )
| 3 |
| A、0 | B、2 | C、1 | D、-1 |