题目内容
14.已知各项均为正数的两个数列{an}和{bn}满足:an+1=$\frac{{a}_{n}+{b}_{n}}{\sqrt{{{a}_{n}}^{2}+{{b}_{n}}^{2}}}$,n∈N*.(1)设bn+1=1+$\frac{{b}_{n}}{{a}_{n}}$,n∈N*,求证:数列{($\frac{{b}_{n}}{{a}_{n}}$)2}是等差数列;
(2)若a1=b1=1,求数列{an}和{bn}的通项公式.
分析 (1)通过将bn+1=$\frac{{a}_{n}+{b}_{n}}{{a}_{n}}$代入an+1=$\frac{{a}_{n}+{b}_{n}}{\sqrt{{{a}_{n}}^{2}+{{b}_{n}}^{2}}}$计算可知$\frac{{b}_{n+1}}{{a}_{n+1}}$=$\sqrt{1+(\frac{{b}_{n}}{{a}_{n}})^{2}}$,进而可知数列{($\frac{{b}_{n}}{{a}_{n}}$)2}是公差为1的等差数列;
(2)通过$(\frac{{b}_{1}}{{a}_{1}})^{2}$=1及(1)可知bn=$\sqrt{n}$an,代入an+1=$\frac{{a}_{n}+{b}_{n}}{\sqrt{{{a}_{n}}^{2}+{{b}_{n}}^{2}}}$计算可知an=$\frac{1+\sqrt{n-1}}{\sqrt{n}}$,进而计算可得结论.
解答 (1)证明:∵bn+1=1+$\frac{{b}_{n}}{{a}_{n}}$=$\frac{{a}_{n}+{b}_{n}}{{a}_{n}}$,
∴an+1=$\frac{{a}_{n}+{b}_{n}}{\sqrt{{{a}_{n}}^{2}+{{b}_{n}}^{2}}}$=$\frac{\frac{{a}_{n}+{b}_{n}}{{a}_{n}}}{\frac{\sqrt{{{a}_{n}}^{2}+{{b}_{n}}^{2}}}{{a}_{n}}}$=$\frac{{b}_{n+1}}{\sqrt{1+(\frac{{b}_{n}}{{a}_{n}})^{2}}}$,
∴$\frac{{b}_{n+1}}{{a}_{n+1}}$=$\sqrt{1+(\frac{{b}_{n}}{{a}_{n}})^{2}}$,
∴$(\frac{{b}_{n+1}}{{a}_{n+1}})^{2}$-$(\frac{{b}_{n}}{{a}_{n}})^{2}$=$[\sqrt{1+(\frac{{b}_{n}}{{a}_{n}})^{2}}]^{2}$-$(\frac{{b}_{n}}{{a}_{n}})^{2}$=1,
∴数列{($\frac{{b}_{n}}{{a}_{n}}$)2}是公差为1的等差数列;
(2)解:∵$(\frac{{b}_{1}}{{a}_{1}})^{2}$=1,
∴$(\frac{{b}_{n}}{{a}_{n}})^{2}$=1+(n-1)=n,
又∵数列{an}和{bn}中各项均为正数,
∴bn=$\sqrt{n}$an,
∴an+1=$\frac{(1+\sqrt{n}){a}_{n}}{\sqrt{{{(1+n)a}_{n}}^{2}}}$=$\frac{1+\sqrt{n}}{\sqrt{n+1}}$,即an=$\frac{1+\sqrt{n-1}}{\sqrt{n}}$,
又∵a1=1满足上式,
∴an=$\frac{1+\sqrt{n-1}}{\sqrt{n}}$;
∴bn=$\sqrt{n}$•$\frac{1+\sqrt{n-1}}{\sqrt{n}}$=1+$\sqrt{n-1}$.
点评 本题考查等差数列的判断与通项,考查运算求解能力,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 8 | B. | 10 | C. | 9或10 | D. | 8和9 |
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
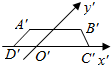 (1)已知△ABC的三边长为a,b,c.判断△ABC的面积与△ABC的平面直观图△A′B′C′的面积的关系.
(1)已知△ABC的三边长为a,b,c.判断△ABC的面积与△ABC的平面直观图△A′B′C′的面积的关系.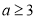 ,函数
,函数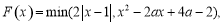 其中
其中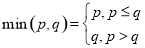 .
. 成立的
成立的 的取值范围;
的取值范围; 的最小值
的最小值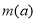 ;
;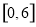 上的最大值
上的最大值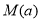 .
.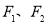 为椭圆
为椭圆 的两个焦点,过
的两个焦点,过 的直线交椭圆于A、B两点若
的直线交椭圆于A、B两点若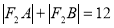 ,则
,则 =_____.
=_____.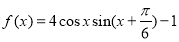 .
.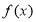 的最小正周期;
的最小正周期;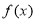 在区间
在区间 上的最大值和最小值
上的最大值和最小值