题目内容
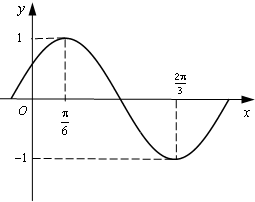 函数f(x)=Asin(ωx+?) (A>0,ω>0,|?|<
函数f(x)=Asin(ωx+?) (A>0,ω>0,|?|<| π |
| 2 |
(Ⅰ)求f(x)的最小正周期及解析式;
(Ⅱ)设g(x)=f(x)-cos2x,求函数g(x)在区间x∈[0,
| π |
| 2 |
分析:(Ⅰ)由图可得A=1,一个周期内最高点与最低点的横坐标之差的绝对值为半个周期,得最小正周期T,进而得ω,代入最高点坐标求φ,得f(x)的解析式;
(Ⅱ)由(Ⅰ)知f(x)的解析式,代入求出g(x)的解析式,用两角和的正弦公式把式中的第一项展开,合并,再逆用两角差的正弦公式把式子变形为一个角的一个三角函数值,由x的范围,得到2x-
的范围,由正弦函数的图象得到sin(2x-
)的最大值和最小值.
(Ⅱ)由(Ⅰ)知f(x)的解析式,代入求出g(x)的解析式,用两角和的正弦公式把式中的第一项展开,合并,再逆用两角差的正弦公式把式子变形为一个角的一个三角函数值,由x的范围,得到2x-
| π |
| 6 |
| π |
| 6 |
解答:解:(Ⅰ)由图可得A=1,
=
-
=
,所以T=π.(2分)
所以ω=2.
当x=
时,f(x)=1,可得sin(2•
+φ)=1,
因为|φ|<
,所以φ=
.(5分)
所以f(x)的解析式为f(x)=sin(2x+
).(6分)
(Ⅱ)g(x)=f(x)-cos2x=sin(2x+
)-cos2x
=sin2xcos
+cos2xsin
-cos2x
=
sin2x-
cos2x=sin(2x-
).(10分)
因为0≤x≤
,所以-
≤2x-
≤
.
当2x-
=
,即x=
时,g(x)有最大值,最大值为1;
当2x-
=-
,即x=0时,g(x)有最小值,最小值为-
.(13分)
| T |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 2 |
所以ω=2.
当x=
| π |
| 6 |
| π |
| 6 |
因为|φ|<
| π |
| 2 |
| π |
| 6 |
所以f(x)的解析式为f(x)=sin(2x+
| π |
| 6 |
(Ⅱ)g(x)=f(x)-cos2x=sin(2x+
| π |
| 6 |
=sin2xcos
| π |
| 6 |
| π |
| 6 |
=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
因为0≤x≤
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
当2x-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
当2x-
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
点评:给出条件求y=Asin(ωx+φ)的解析式,条件不管以何种方式给出,一般先求A,再求ω,最后求φ;求三角函数最值时,一般要把式子化为y=Asin(ωx+φ)的形式,从x的范围由里向外扩,一直扩到Asin(ωx+φ)的范围,结合正弦函数图象求出最值.

练习册系列答案
相关题目
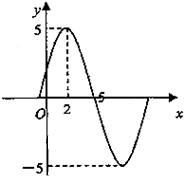 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,x∈R,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,x∈R,|φ|<| π |
| 2 |
A、f(x)=5sin(
| ||||
B、f(x)=5sin(
| ||||
C、f(x)=5sin(
| ||||
D、f(x)=5sin(
|
 已知函数
已知函数 (2013•大连一模)已知函数
(2013•大连一模)已知函数 当
当 函数
函数