题目内容
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF= ,CE=2
,CE=2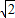 ,CE∥AF,AC⊥CE,
,CE∥AF,AC⊥CE,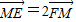
(I)求证:CM∥平面BDF;
(II)求异面直线CM与FD所成角的余弦值的大小;
(III)求二面角A-DF-B的大小.

【答案】分析:(I) 可知CD、CB、CE两两垂直.建立如图空间直角坐标系C-xyz.利用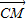 与
与 平行证出CM∥OF,则可以证出CM∥平面BDF
平行证出CM∥OF,则可以证出CM∥平面BDF
(II) 利用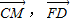 的夹角求异面直线CM与FD所成角
的夹角求异面直线CM与FD所成角
(III)先求出平面ADF与平面BDF的一个法向量,利用两法向量的夹角求出二面角A-DF-B的大小.
解答:解:(I)证明:因为面ABCD⊥面ACEF,面ABCD∩面ACEF=AC,且AC⊥CE,∴CE⊥面ABCD.
所以CD、CB、CE两两垂直.可建立如图空间直角坐标系C-xyz.
则(2,0,0),A(2,2,0),B(0,2,0),F(2,2, ),O(1,1,0)…(2分)
),O(1,1,0)…(2分)
由 ,可求得M(
,可求得M( )…(3分)
)…(3分)
 =(
=( ),
), ).
).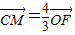
所以 ∥
∥ ,
,
∴CM∥OF…(5分)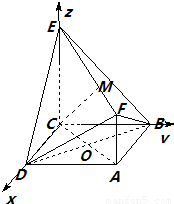
(II)因为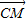 =(
=( ),
),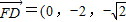 ),
),
所以cos< >=
>=
异面直线CM与FD所成角的余弦值的大小为 …(8分)
…(8分)
(III)因为CD⊥平面ADF,所以平面ADF的法向量 =(2,0,0).
=(2,0,0).
设平面BDF的法向量为 =(x,y,1)…(9分)
=(x,y,1)…(9分)
由 .
.
所以法向量 =(-
=(- ,1)…(10分)
,1)…(10分)
所以
所以<
 =
= ,…(11分)
,…(11分)
由图可知二面角A-DF-B为锐角,
所以二面角A-DF-B大小为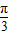 .…(12分)
.…(12分)
点评:本题考查直线和平面平行的判定,异面直线夹角,二面角的计算,利用了空间向量的方法.要注意相关点和向量坐标的准确性,及转化时角的相等或互余关系.
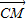 与
与 平行证出CM∥OF,则可以证出CM∥平面BDF
平行证出CM∥OF,则可以证出CM∥平面BDF (II) 利用
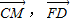 的夹角求异面直线CM与FD所成角
的夹角求异面直线CM与FD所成角(III)先求出平面ADF与平面BDF的一个法向量,利用两法向量的夹角求出二面角A-DF-B的大小.
解答:解:(I)证明:因为面ABCD⊥面ACEF,面ABCD∩面ACEF=AC,且AC⊥CE,∴CE⊥面ABCD.
所以CD、CB、CE两两垂直.可建立如图空间直角坐标系C-xyz.
则(2,0,0),A(2,2,0),B(0,2,0),F(2,2,
 ),O(1,1,0)…(2分)
),O(1,1,0)…(2分)由
 ,可求得M(
,可求得M( )…(3分)
)…(3分) =(
=( ),
), ).
).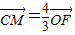
所以
 ∥
∥ ,
,∴CM∥OF…(5分)

(II)因为
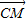 =(
=( ),
),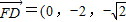 ),
),所以cos<
 >=
>=
异面直线CM与FD所成角的余弦值的大小为
 …(8分)
…(8分)(III)因为CD⊥平面ADF,所以平面ADF的法向量
 =(2,0,0).
=(2,0,0).设平面BDF的法向量为
 =(x,y,1)…(9分)
=(x,y,1)…(9分)由
 .
.所以法向量
 =(-
=(- ,1)…(10分)
,1)…(10分)所以

所以<

 =
= ,…(11分)
,…(11分)由图可知二面角A-DF-B为锐角,
所以二面角A-DF-B大小为
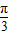 .…(12分)
.…(12分)点评:本题考查直线和平面平行的判定,异面直线夹角,二面角的计算,利用了空间向量的方法.要注意相关点和向量坐标的准确性,及转化时角的相等或互余关系.

练习册系列答案
相关题目
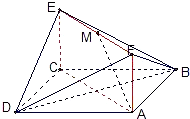 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=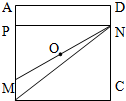 如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当
如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=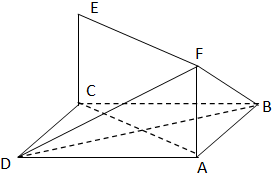 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, (2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.