题目内容
【题目】已知函数![]() .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求证:当![]() 时,
时, ![]() ;
;
(Ⅲ)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析;(Ⅲ)1.
;(Ⅱ)见解析;(Ⅲ)1.
【解析】试题分析:
(1)对函数求导,利用导数研究函数的切线方程即可;
(2)令![]() ,问题转化为证明
,问题转化为证明![]() ,证得
,证得![]() 即可.
即可.
(3)令![]() ,讨论函数
,讨论函数![]() 的性质结合恒成立的性质即可求得最终结果.
的性质结合恒成立的性质即可求得最终结果.
试题解析:
(Ⅰ)![]() ,
, ![]() ,
,
又![]() ,所以切线方程为
,所以切线方程为![]() ;
;
(Ⅱ)由题意知![]() ,令
,令![]()
![]() .
.
![]()
令![]() ,解得
,解得![]() .
.
易知当![]() 时,
时, ![]() ,易知当
,易知当![]() 时,
时, ![]() .
.
即![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
所以![]() ,
, ![]()
即![]() ,即
,即![]() .
.
(Ⅲ)设![]() ,依题意,对于任意
,依题意,对于任意![]() ,
, ![]() 恒成立.
恒成立.
![]() ,
,
![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时, ![]() ,满足题意.
,满足题意.
![]() 时,随
时,随![]() 变化,
变化, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| — | 0 | + |
| ↘ | 极小值 | ↗ |
![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]()
即当![]() 时,总存在
时,总存在![]() ,不合题意.
,不合题意.
综上所述,实数![]() 的最大值为1.
的最大值为1.

【题目】4月23日是世界读书日,惠州市某中学在此期间开展了一系列的读书教育活动。为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,且将日均课外阅读时间不低于60分钟的学生称为“读书迷”,低于60分钟的学生称为“非读书迷”.
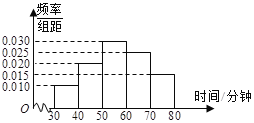
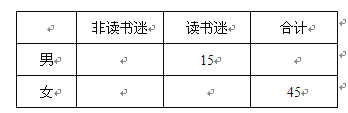
(Ⅰ)根据已知条件完成下面2×2列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
(Ⅱ)将频率视为概率,现在从该校大量学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中“读书迷”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、数学期望
的分布列、数学期望![]() 和方差
和方差![]() .
.
附: 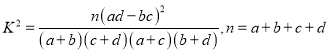
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】(本小题满分12分)某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据如表1所示
表1
参加社团活动 | 不参加社团活动 | 合计 | |
学习积极性高 | 17 | 8 | 25 |
学习积极性一般 | 5 | 20 | 25 |
合计 | 22 | 28 | 50 |
(1)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
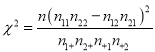
【题目】某品牌汽车的![]() 店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 |
|
|
(1)若以上表计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3为顾客,求事件![]() :“至多有1位采用分6期付款“的概率
:“至多有1位采用分6期付款“的概率![]() ;
;
(2)按分层抽样方式从这100为顾客中抽取5人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.