题目内容

异面直线a、b所成的角为80°，过空间一点P作直线l，若l与a、b所成的角都是60°，则这样的直线l共有 ______条．

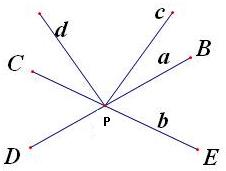
精英家教网
先将异面直线a，b平移到点P，则∠BPE=80°，∠EPD=100°
而∠BPE的角平分线与a和b的所成角为40°，
而∠EPD的角平分线与a和b的所成角为50°
∵60°＞40°，60°＞50°
∴直线与a，b所成的角相等且等于60°有且只有4条，
使直线在面BPE的射影为∠BPE的角平分线，
和直线在面EPD的射影为∠EPD的角平分线，
故答案为：4．
练习册系列答案
相关题目
5、已知异面直线a与b所成的角为50°，P为空间一点，则过点P与a、b所成的角都是300的直线有且仅有（　　）
已知两条异面直线a，b所成的角为
π
3
，直线l与a，直线l与b所成的角为θ，则θ的范围是（　　）
A、[
π
6
，
π
2
]
B、[
π
3
，
π
2
]
C、[
π
6
，
5π
6
]
D、[
π
3
，
2π
3
]
已知：两条异面直线a、b所成的角为θ，它们的公垂线段AA1的长度为d．在直线a、b上分别取点E、F，设A1E=m，AF=n．求证：EF=
d2+m2+n2±2mncosθ
．
（2010•南充一模）已知两异面直线a，b所成的角为
π
3
，直线l分别与a，b所成的角都是θ，则θ的取值范围是
[
π
6
，
π
2
]
[
π
6
，
π
2
]
．
设异面直线a、b所成的角为
π
3
，经过空间一点O有且只有一条直线l与异面直线a、b成等角θ，则θ的值为
π
6
或
π
2
π
6
或
π
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网