题目内容
(12分)已知函数![]()
![]() ,
,![]() ,
,
(Ⅰ)当![]() 时,求
时,求![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)若![]() 是
是![]() 两个极值点,且
两个极值点,且![]() ,求证
,求证![]() ;
;
(Ⅲ)若![]() 是奇函数,且当
是奇函数,且当![]() 时,
时,![]() 有两个不同的实根,求
有两个不同的实根,求![]() 的取值范围
的取值范围
![]() 解析:(1)当
解析:(1)当![]() 时,
时,![]()
![]() ,由
,由![]() 得:
得:![]()
所以![]() 的单调增区间为
的单调增区间为![]() ………………4分
………………4分
(2)![]() 若
若![]() ,则满足
,则满足
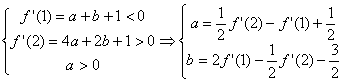
![]() ………………9分
………………9分
(3)由![]() 为奇函数得:
为奇函数得:![]()
当![]() ,由
,由![]() 得,
得,![]()
令![]() ,若
,若![]() 有两个不同的实数根,
有两个不同的实数根,
则满足![]() 与
与![]() 在
在![]() 有两个不同的交点,
有两个不同的交点,
![]()
所以当![]() ,
,![]() 为单调增函数,
为单调增函数,
当![]() ,
,![]() 为单调减函数
为单调减函数
![]() ,
,![]() ,又因为
,又因为![]()

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 的定义域为集合A,
的定义域为集合A,  的值域为集合B.
的值域为集合B. ,求
,求 ;
; ,求实数
,求实数 的取值范围。
的取值范围。 的导函数
的导函数 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上.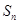 的最大值;
的最大值; ,其中
,其中 ,求
,求 的前
的前 是偶函数.
是偶函数. 有解,求m的取值范围.
有解,求m的取值范围.