题目内容
7. 如图,$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上任一点,F1,F2为椭圆的左、右焦点,求|PF1|的 最大值和最小值.
如图,$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上任一点,F1,F2为椭圆的左、右焦点,求|PF1|的 最大值和最小值.
分析 设椭圆的焦距为2c,即有c=$\sqrt{{a}^{2}-{b}^{2}}$,设出左焦点和左准线,运用椭圆的第二定义,可得|PF1|=ed,再由椭圆的范围,即可得到最值.
解答 解:设椭圆的焦距为2c,
即有c=$\sqrt{{a}^{2}-{b}^{2}}$,
设左焦点为(-c,0),左准线为x=-$\frac{{a}^{2}}{c}$,
离心率e=$\frac{c}{a}$,
即有|PF1|=ed(d为左焦点到左准线的距离)
=$\frac{c}{a}$(xP+$\frac{{a}^{2}}{c}$)=a+$\frac{c}{a}$•xP,
当xP=a时取得最大值a+c,即a+$\sqrt{{a}^{2}-{b}^{2}}$;
当xP=-a时取得最小值a-c,即a-$\sqrt{{a}^{2}-{b}^{2}}$.
点评 本题考查椭圆的定义、方程和性质,考查椭圆的范围及运用,注意焦半径公式的运用,属于中档题.

练习册系列答案
相关题目
 把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:2,母线长10cm.圆台侧面展开是一个$\frac{1}{4}$圆环,求:
把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:2,母线长10cm.圆台侧面展开是一个$\frac{1}{4}$圆环,求: 如图,在正棱柱ABC-A1B1C1中,E,F分别为线段AA1,C1B的中点,求证:EF∥平面ABC.
如图,在正棱柱ABC-A1B1C1中,E,F分别为线段AA1,C1B的中点,求证:EF∥平面ABC.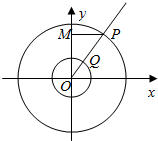 如图所示,以原点O为圆心的两个同心圆的半径分别为3和1,过原点O的射线交大圆于点P,交小圆于点Q,P在y轴上的射影为M,动点N满足$\overrightarrow{PM}$=λ$\overrightarrow{PN}$且$\overrightarrow{PM}$•$\overrightarrow{QN}$=0.
如图所示,以原点O为圆心的两个同心圆的半径分别为3和1,过原点O的射线交大圆于点P,交小圆于点Q,P在y轴上的射影为M,动点N满足$\overrightarrow{PM}$=λ$\overrightarrow{PN}$且$\overrightarrow{PM}$•$\overrightarrow{QN}$=0.