题目内容
如图,四棱锥 中,
中, ,底面
,底面 为梯形,
为梯形, ,
, ,且
,且
 .(10分)
.(10分)

(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
 中,
中, ,底面
,底面 为梯形,
为梯形, ,
, ,且
,且
 .(10分)
.(10分)
(1)求证:
 ;
;(2)求二面角
 的余弦值.
的余弦值.(1)证明见解析;(2)二面角 的余弦值为
的余弦值为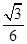 .
.
 的余弦值为
的余弦值为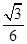 .
.试题分析:(1)连结
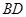 ,交
,交 于点
于点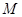 ,连结
,连结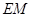 ,由所给条件可得
,由所给条件可得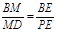 ,即
,即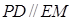 ,则
,则 ;(2)以
;(2)以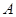 为原点,
为原点,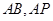 所在直线分别为
所在直线分别为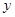 轴、
轴、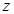 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.设
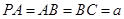 ,则可得
,则可得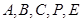 坐标,设
坐标,设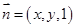 为平面
为平面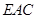 的一个法向量,由
的一个法向量,由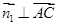
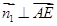 ,可得
,可得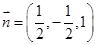 ,同理
,同理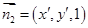 为平面
为平面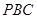 的一个法向量,
的一个法向量,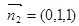 ,
, 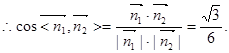 知二面角的余弦值.
知二面角的余弦值.试题解析:(1)连结
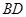 ,交
,交 于点
于点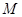 ,连结
,连结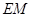 , ∵
, ∵ ,
,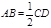 , ∴
, ∴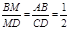
又 ∵
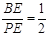 , ∴
, ∴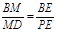 ∴ 在△BPD中,
∴ 在△BPD中,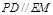
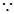
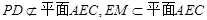 ∴
∴ ∥平面
∥平面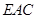 ----------------4分
----------------4分
(2)方法一:以
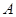 为原点,
为原点,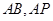 所在直线分别为
所在直线分别为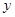 轴、
轴、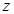 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.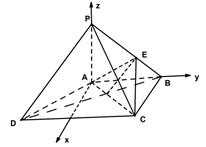
设
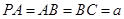 ,则
,则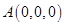 ,
,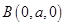 ,
,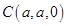 ,
,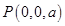 ,
,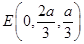 .
.设
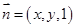 为平面
为平面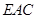 的一个法向量,
的一个法向量,则
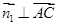 ,
,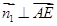 ,∴
,∴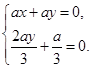 ,
,解得
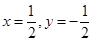 ,∴
,∴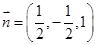 .
.设
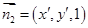 为平面
为平面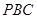 的一个法向量,则
的一个法向量,则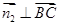 ,
,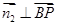 ,
,又
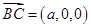 ,
,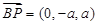 ,∴
,∴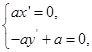 ,
,解得
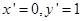 ,∴
,∴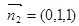
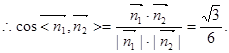
∴二面角
 的余弦值为
的余弦值为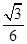 .-------------------10分
.-------------------10分方法二:在等腰Rt
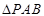 中,取
中,取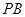 中点
中点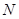 ,连结
,连结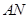 ,则
,则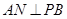
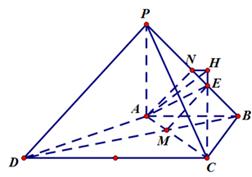
∵面
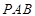 ⊥面
⊥面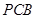 ,面
,面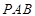
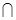 面
面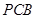 =
=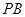 ,∴
,∴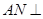 平面
平面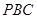 .
.在平面
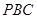 内,过
内,过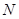 作
作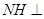 直线
直线 于
于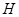 ,连结
,连结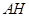 ,由
,由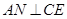 、
、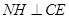 ,
,得
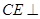 平面
平面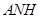 ,故
,故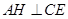 .
.∴
 就是二面角
就是二面角 的平面角.
的平面角.在
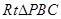 中,设
中,设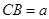 ,
,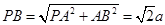 ,
, ,
,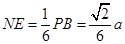 ,
,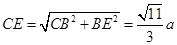 ,
,由
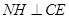 ,
,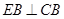 可知:
可知: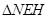 ∽
∽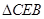 ,
,∴
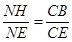 , 代入解得:
, 代入解得: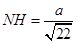 .
.在
 中,
中,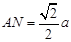 ,
,∴
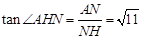 ,
,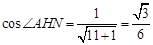 .
.∴二面角
 的余弦值为
的余弦值为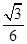 .
.
练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
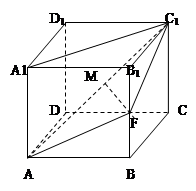
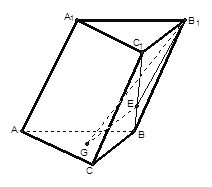
 中,侧面
中,侧面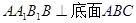 ,
,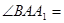
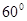 ,
,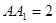 ,底面
,底面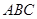 是边长为
是边长为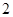 的正三角形,其重心为
的正三角形,其重心为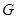 点,
点,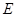 是线段
是线段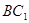 上一点,且
上一点,且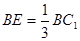 .
.
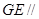 侧面
侧面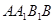 ;
;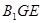 与底面
与底面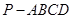 中,底面
中,底面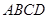 是平行四边形,
是平行四边形,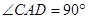 ,
,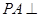 平面
平面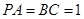 ,
,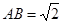 ,
,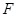 是
是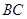 的中点.
的中点.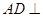 平面
平面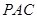 ;
; 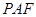 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.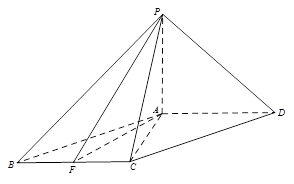
 中,侧面
中,侧面 为菱形,
为菱形, .
.
 ;
; ,
, ,
, ,求二面角
,求二面角 的余弦值.
的余弦值. ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, ,
,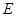 分别是
分别是 的中点,
的中点, .
.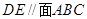 ;
;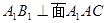 ;
; 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.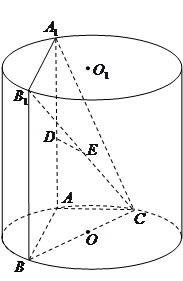
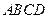 的长方体被截面
的长方体被截面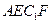 所截面而得到的,其中
所截面而得到的,其中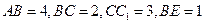 .
.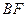 的长;
的长;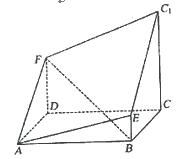
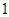 的正方体
的正方体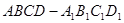 中,
中,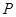 为线段
为线段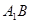 上的动点,则下列结论错误的是
上的动点,则下列结论错误的是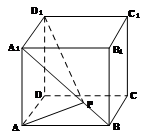
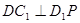
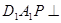 平面
平面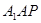
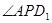 的最大值为
的最大值为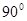
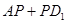 的最小值为
的最小值为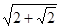
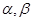 是两个不同的平面,
是两个不同的平面,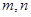 是平面
是平面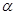 及
及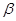 之外的两条不同直线,给出四个论断:
之外的两条不同直线,给出四个论断: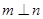 ②
②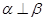 ③
③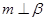 ④
④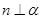 。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.
。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.