题目内容
已知平面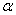 截一球面得圆M,过圆心M且与
截一球面得圆M,过圆心M且与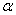 成
成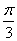 角的平面
角的平面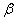 截该球面得圆N若圆M、圆N面积分别为4
截该球面得圆N若圆M、圆N面积分别为4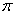 、13
、13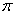 ,则球面面积为
,则球面面积为
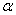 截一球面得圆M,过圆心M且与
截一球面得圆M,过圆心M且与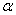 成
成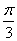 角的平面
角的平面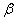 截该球面得圆N若圆M、圆N面积分别为4
截该球面得圆N若圆M、圆N面积分别为4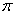 、13
、13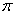 ,则球面面积为
,则球面面积为A.36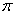 | B.48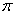 | C.64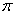 | D.100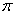 |
C
试题分析:圆M的半径为2,球心到圆M的距离为
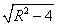 ,圆N的半径为
,圆N的半径为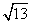 ,球心到圆N的距离为
,球心到圆N的距离为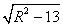 ,因为两圆平面所成的角为
,因为两圆平面所成的角为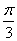 ,所以两距离垂线的夹角为
,所以两距离垂线的夹角为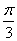 ,所以
,所以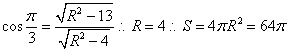
点评:球面面积
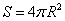 ,两圆面所成二面角的大小等于其法向量的夹角,球的截面圆半径,球心到截面圆的距离及球的半径构成直角三角形
,两圆面所成二面角的大小等于其法向量的夹角,球的截面圆半径,球心到截面圆的距离及球的半径构成直角三角形
练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
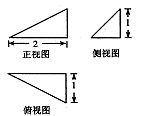
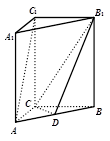
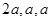 ,其顶点都在一个球面上,则该球的表面积为( )
,其顶点都在一个球面上,则该球的表面积为( )



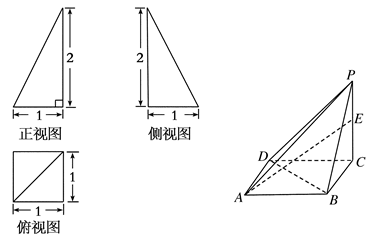
 ABC为正三角形,
ABC为正三角形,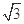 ,M为PA的中点,N在线段PD上。
,M为PA的中点,N在线段PD上。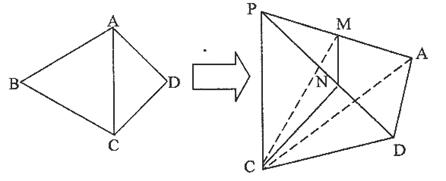
 平面CMN,求证:AD//平面CMN;
平面CMN,求证:AD//平面CMN;