题目内容
如图,在直三棱柱ABC-A1B1C1中,底面为等腰直角三角形,AC⊥BC,点D是AB的中点,侧面BB1C1C是正方形.
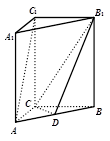
(1) 求证AC⊥B1C;(2)求二面角B-CD-B1平面角的正切值.

(1) 求证AC⊥B1C;(2)求二面角B-CD-B1平面角的正切值.
(1)要证明线线垂直,要通过线面垂直的性质定理来求解,主要是得到AC⊥平面BCC1B1。
(2)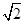
(2)
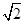
试题分析:证明:(1)在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,
∴CC1⊥AC,
又AC⊥BC,BC∩CC1=C,
所以,AC⊥平面BCC1B1,
所以,AC⊥B1C. 3分
(2)∵△ABC是等腰直角三角形,D为AB中点,
∴CD⊥AB
∵平面ABC⊥平面AA1B1B,平面ABC∩平面AA1B1B=AB,
∴CD ⊥平面AA1B1B,
∵B1D
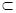 平面AA1B1B,BD
平面AA1B1B,BD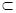 平面AA1B1B,
平面AA1B1B,∴CD⊥B1D,CD⊥BD,
∴∠B1DB是二面角B-CD-B1平面角, 6分
不妨设正方形BB1C1C的棱长为2a,则:
在RT△B1DB中,BD=
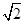 a,BB1=2a,∠B1BD=90º
a,BB1=2a,∠B1BD=90º∴tan∠B1DB=
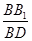 =
=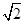 .
.∴所求二面角B-CD-B1平面角的正切值为
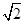 . 8分
. 8分点评:考查了线线垂直和二面角的平面角的求解,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



 截一球面得圆M,过圆心M且与
截一球面得圆M,过圆心M且与 角的平面
角的平面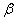 截该球面得圆N若圆M、圆N面积分别为4
截该球面得圆N若圆M、圆N面积分别为4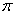 、13
、13




 =8,则过P且平行于底面的截面的面积为______.
=8,则过P且平行于底面的截面的面积为______.