题目内容
6.设函数f(x)=(x-1)2ex.(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求f(x)的单调区间和极值.
分析 (1)先求出函数f(x)的导数,求出其在x=0处的斜率,从而求出切线方程;(2)解关于导函数的不等式,得到函数的单调区间,从而求出函数的极值.
解答 解:(1)∵f(0)=1,∴切点为(0,1),
∵f′(x)=2(x-1)ex+(x-1)2ex
=ex(x2-1),
∴f′(0)=-1,
∴切线方程是y-1=-x,即:x+y-1=0;
(2)由f′(x)=ex(x2-1),
令f′(x)>0,解得:x>1或x<-1,
令f′(x)<0,解得:-1<x<1,
∴函数f(x)在(-∞,-1),(1,+∞)单调递增,在(-1,1)单调递减,
∴f(x)极大值=f(-1)=$\frac{2}{e}$,f(x)极小值=f(1)=0.
点评 本题考查了函数的单调性,函数的最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
17.平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,$\overrightarrow{a}$=(1,$\sqrt{3}$),|$\overrightarrow{b}$|=1,则|$\overrightarrow{a}+2\overrightarrow{b}$|等于( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 12 |
15.过抛物线C:x2=4y的焦点作垂直于对称轴的直线l,在第一象限内与C交于点P,则抛物线在点P处的切线方程为( )
| A. | x-2y=0 | B. | 2x-y-3=0 | C. | x-y+1=0 | D. | x-y-1=0 |
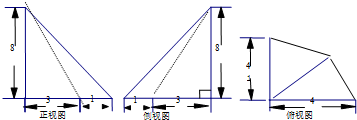 已知某空间几何体的三视图如图所示,则该几何体的体积是32.
已知某空间几何体的三视图如图所示,则该几何体的体积是32.