题目内容
设椭圆 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,离心率为
,离心率为 ,在
,在 轴负半轴上有一点
轴负半轴上有一点 ,且
,且
(Ⅰ)若过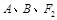 三点的圆恰好与直线
三点的圆恰好与直线 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(Ⅱ)在(Ⅰ)的条件下,过右焦点 作斜率为
作斜率为 的直线
的直线 与椭圆C交于
与椭圆C交于 两点,在
两点,在 轴上是否存在点
轴上是否存在点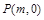 ,使得以
,使得以 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出 的取值范围;否则,请说明理由.
的取值范围;否则,请说明理由.

【答案】
(Ⅰ)
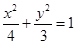 (Ⅱ)
(Ⅱ) 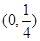
【解析】本试题主要是考查了椭圆的方程与性质和直线与椭圆的位置关系的运用。
(1)由题意结合点到直线的距离公式和椭圆的性质得到椭圆方程的求解。
(2)设直线方程与椭圆联立,得到关于x的一元二次方程,结合韦达定理和向量的关系式得到参数m与k的关系式。进而求解参数的范围。
解:(1)由题意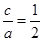 ,得
,得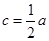
 ,所以
,所以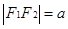
又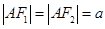 由于
由于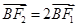 ,所以
,所以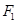 为
为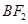 的中点,
的中点,
所以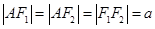
所以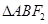 的外接圆圆心为
的外接圆圆心为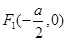 ,半径
,半径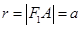 …………………3分
…………………3分
又过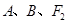 三点的圆与直线
三点的圆与直线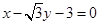 相切,
相切,
所以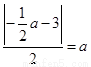 解得
解得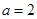 ,
,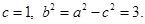
所求椭圆方程为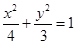 …………………………………………………… 6分
…………………………………………………… 6分
(2)有(1)知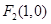 ,设
,设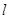 的方程为:
的方程为: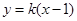
将直线方程与椭圆方程联立 ,整理得
,整理得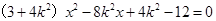
设交点为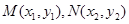 ,因为
,因为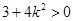
则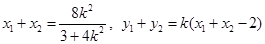 ……………………………………8分
……………………………………8分
若存在点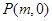 ,使得以
,使得以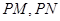 为邻边的平行四边形是菱形,
为邻边的平行四边形是菱形,
由于菱形对角线垂直,所以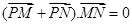
又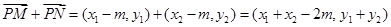
又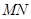 的方向向量是
的方向向量是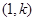 ,故
,故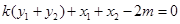 ,则
,则
 ,即
,即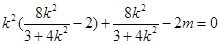
由已知条件知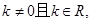
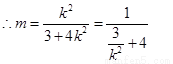 ………………………11分
………………………11分
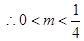 ,故存在满足题意的点
,故存在满足题意的点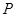 且
且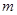 的取值范围是
的取值范围是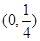 ………………13分
………………13分

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目

 的左、右焦点分别是F1、F2,离心率
的左、右焦点分别是F1、F2,离心率 ,右准线l上的两动点M、N,且
,右准线l上的两动点M、N,且 ,
, ,求a、b的值;
,求a、b的值; 最小时,求证
最小时,求证 与
与 共线。
共线。 
 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.
,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.