题目内容
已知椭圆C:
+
=1(a>b>0),
(1)若椭圆的长轴长为4,离心率为
,求椭圆的标准方程;
(2)在(1)的条件下,设过定点M(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角(O为坐标原点),求直线l的斜率k的取值范围;
(3)过原点O任意作两条互相垂直的直线与椭圆C:
+
=1(a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR的一边距离为d,试求d=1时a,b满足的条件.
| x2 |
| a2 |
| y2 |
| b2 |
(1)若椭圆的长轴长为4,离心率为
| ||
| 2 |
(2)在(1)的条件下,设过定点M(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角(O为坐标原点),求直线l的斜率k的取值范围;
(3)过原点O任意作两条互相垂直的直线与椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
分析:(1)由题意可得
,解得即可;
(2)直线l的方程为y=kx+2,设A(x1,y1),B(x2,y2).与椭圆方程联立,由△>0,解得k的取值范围.可得根与系数的关系.
若∠AOB为锐角,则
•
>0,把根与系数的关系代入又得到k的取值范围,取其交集即可.
(3)如图所示,设P(x1,y1),Q(x2,y2),S(-x1,-y1),R(-x2,-y2).
①当直线PS与QR的斜率都存在时,设直线PS:y=kx,则直线QR:y=-
x.与椭圆方程联立解得
,
.直线PR的斜率存在时,则直线PR:y-y1=
(x-x1),化为(y2-y1)x+(x1-x2)y+x2y1-x1y2=0.由于d=1,利用点到直线的距离公式可得
=1,化简并代入即可化为a2b2=a2+b2.
②当直线PS与QR的斜率有一个不存在时,直线PR的斜率不存在时,经验证上式也成立.
|
(2)直线l的方程为y=kx+2,设A(x1,y1),B(x2,y2).与椭圆方程联立,由△>0,解得k的取值范围.可得根与系数的关系.
若∠AOB为锐角,则
| OA |
| OB |
(3)如图所示,设P(x1,y1),Q(x2,y2),S(-x1,-y1),R(-x2,-y2).
①当直线PS与QR的斜率都存在时,设直线PS:y=kx,则直线QR:y=-
| 1 |
| k |
| x | 2 1 |
| x | 2 2 |
| y2-y1 |
| x2-x1 |
| |x2y1-x1y2| | ||
|
②当直线PS与QR的斜率有一个不存在时,直线PR的斜率不存在时,经验证上式也成立.
解答:解:(1)由题意可得
,解得a2=4,b2=1,c=
.∴椭圆的标准方程为
+y2=1;
(2)直线l的方程为y=kx+2,设A(x1,y1),B(x2,y2).联立
,化为(1+4k2)x2+16kx+12=0,由△=162k2-48(1+4k2)>0,解得k>
或k<-
.∴x1+x2=
,x1x2=
.
若∠AOB为锐角,则
•
>0,得x1x2+y1y2=x1x2+(kx1+2)(kx2+2)=(1+k2)x1x2+2k(x1+x2)+4>0,代入得
+
+4>0,化为k2<4,解得-2<k<2.∴直线l的斜率k的取值范围为{x|-2<k<2}∩{x|k<-
或k>
}={k|-2<k<-
或
<x<2}.
(3)如图所示,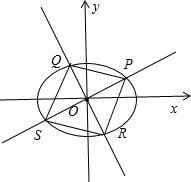 设P(x1,y1),Q(x2,y2),S(-x1,-y1),R(-x2,-y2).
设P(x1,y1),Q(x2,y2),S(-x1,-y1),R(-x2,-y2).
①当直线PS与QR的斜率都存在时,设直线PS:y=kx,则直线QR:y=-
x.
联立
,解得
=
.(*)
联立
,解得
=
.(**)
直线PR的斜率存在时,则直线PR:y-y1=
(x-x1),化为(y2-y1)x+(x1-x2)y+x2y1-x1y2=0.
∵d=1,∴
=1,
代入化为:(k+
)2
=k2
+
+
+
.
把(*)(**)代入上式:
•
=
+
+
+
.
化为a2b2=a2+b2.
即
+
=1为定值.
②当直线PS与QR的斜率有一个不存在时,直线PR的斜率不存在时,经验证上式也成立.
|
| 3 |
| x2 |
| 4 |
(2)直线l的方程为y=kx+2,设A(x1,y1),B(x2,y2).联立
|
| ||
| 2 |
| ||
| 2 |
| -16k |
| 1+4k2 |
| 12 |
| 1+4k2 |
若∠AOB为锐角,则
| OA |
| OB |
| 12(1+k2) |
| 1+4k2 |
| -32k2 |
| 1+4k2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(3)如图所示,
 设P(x1,y1),Q(x2,y2),S(-x1,-y1),R(-x2,-y2).
设P(x1,y1),Q(x2,y2),S(-x1,-y1),R(-x2,-y2).①当直线PS与QR的斜率都存在时,设直线PS:y=kx,则直线QR:y=-
| 1 |
| k |
联立
|
| x | 2 1 |
| a2b2 |
| b2+a2k2 |
联立
|
| x | 2 2 |
| a2b2k2 |
| a2+b2k2 |
直线PR的斜率存在时,则直线PR:y-y1=
| y2-y1 |
| x2-x1 |
∵d=1,∴
| |x2y1-x1y2| | ||
|
代入化为:(k+
| 1 |
| k |
| x | 2 1 |
| x | 2 2 |
| x | 2 1 |
| 1 |
| k2 |
| x | 2 2 |
| x | 2 1 |
| x | 2 2 |
把(*)(**)代入上式:
| (k2+1)2 |
| k2 |
| a4b4k2 |
| (a2+b2k2)(b2+a2k2) |
| a2b2k2 |
| b2+a2k2 |
| a2b2 |
| a2+b2k2 |
| a2b2 |
| b2+a2k2 |
| a2b2k2 |
| a2+b2k2 |
化为a2b2=a2+b2.
即
| 1 |
| a2 |
| 1 |
| b2 |
②当直线PS与QR的斜率有一个不存在时,直线PR的斜率不存在时,经验证上式也成立.
点评:熟练掌握椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立、直线的点斜式、分类讨论思想方法等是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目