题目内容
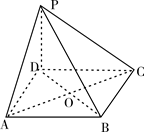
如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=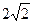 .
.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求点C到平面PBD的距离.
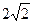 .
.(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求点C到平面PBD的距离.

证:(Ⅰ)在Rt△BAD中,AD=2,BD=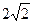 ,
,
∴AB=2,ABCD为正方形,因此BD⊥AC. …………2分
∵PA⊥平面ABCD,BDÌ平面ABCD, ∴BD⊥PA .
又∵PA∩AC=A∴BD⊥平面PAC. …………7分
(Ⅱ)∵PA=AB=AD=2∴PB=PD=BD=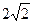 …………8分
…………8分
设C到面PBD的距离为d,由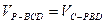 ,…………10分
,…………10分
有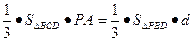 , …………11分
, …………11分
即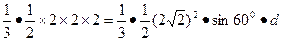 ,…………12分
,…………12分
得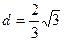 ………14分
………14分
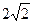 ,
,∴AB=2,ABCD为正方形,因此BD⊥AC. …………2分
∵PA⊥平面ABCD,BDÌ平面ABCD, ∴BD⊥PA .
又∵PA∩AC=A∴BD⊥平面PAC. …………7分
(Ⅱ)∵PA=AB=AD=2∴PB=PD=BD=
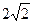 …………8分
…………8分设C到面PBD的距离为d,由
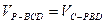 ,…………10分
,…………10分有
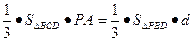 , …………11分
, …………11分 即
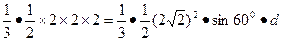 ,…………12分
,…………12分得
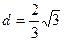 ………14分
………14分 略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
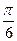 B.
B.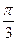 C.
C.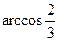 D.
D.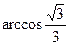
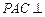 平面
平面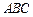 ,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO
,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO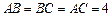 ,
,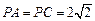 .求证:
.求证: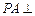 平面
平面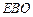 ;
; ∥平面
∥平面

 所在的平面与平面
所在的平面与平面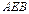 垂直,且
垂直,且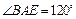 ,
,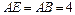 ,
,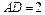 ,
,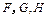 分别为
分别为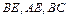 的中点.
的中点.
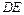 与平面
与平面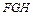 平行;
平行;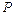 在直线
在直线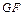 上,且二面角
上,且二面角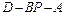 的大小为
的大小为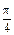 ,试确定点
,试确定点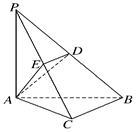 (2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值; 平面ABC,EB//DC,AC=BC=EB=2DC=2,
平面ABC,EB//DC,AC=BC=EB=2DC=2, ,P、Q分别为DE、AB的中点。
,P、Q分别为DE、AB的中点。
 ,M是BC的中点,点N在C1C上。
,M是BC的中点,点N在C1C上。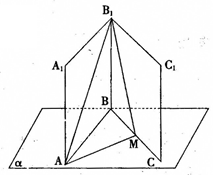
 N的位置,使
N的位置,使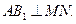
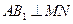 时,求二面角M—AB1—N的余弦值。
时,求二面角M—AB1—N的余弦值。 底面ABCD,PD=AD
底面ABCD,PD=AD