题目内容
在△ABC中,角A、B、C所对的边分别为a、b、c,则满足b=2a,A=25°的△ABC的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:正弦定理
专题:解三角形
分析:根据题意和正弦值的大小确定bsinA<a<b,从而判断出△ABC的个数.
解答:
解:由题意得,b=2a,A=25°,
则h=bsinA=bsin25°<bsin30°=
b=a,
所以bsinA<a<b,
则满足条件的三角形的个数为2,
故选:C.
则h=bsinA=bsin25°<bsin30°=
| 1 |
| 2 |
所以bsinA<a<b,
则满足条件的三角形的个数为2,
故选:C.
点评:本题考查了正弦定理及应用,以及三角形的解的个数,属于基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
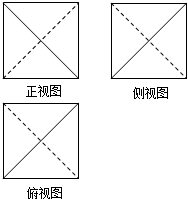 某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )
某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )A、
| ||||
| B、3π | ||||
| C、π | ||||
D、
|