题目内容
（2007•杨浦区二模）已知正四棱锥的底面面积为4cm2，体积为4cm3，设它的侧面上的斜高与底面所成角的大小为θ，则sinθ的值是
．
．．
3
| ||
| 10 |
3
| ||
| 10 |
分析：设E为CD中点，由正棱锥性质，斜高PE⊥CD，，OE⊥CD，∠PEO为斜高与底面所成角，∠PEO=θ．在直角三角形POE中求出即可．
解答：解：如图，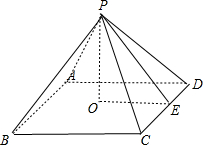
底面面积为4cm2，底面边长CD=2，．体积为4cm3，高PO=3，
E为CD中点，由正棱锥性质，斜高PE⊥CD，，OE⊥CD，∠PEO为斜高与底面所成角，∠PEO=θ．
在直角三角形POE中，sinθ=
=
=
．
故答案为：
．
底面面积为4cm2，底面边长CD=2，．体积为4cm3，高PO=3，E为CD中点，由正棱锥性质，斜高PE⊥CD，，OE⊥CD，∠PEO为斜高与底面所成角，∠PEO=θ．
在直角三角形POE中，sinθ=
| PO |
| PE |
| 3 | ||
|
3
| ||
| 10 |
故答案为：
3
| ||
| 10 |
点评：本题考查线面角的计算，要将空间角转化成平面角来解决．考查空间想象，转化、计算能力．
练习册系列答案
相关题目