题目内容
已知向量
=(cos
x,sin
x),
=(cos
,-sin
),且x∈[
,
π]
(1)求|
+
|的取值范围;
(2)求函数f(x)=
•
-|
+
|的最小值,并求此时x的值.
| a |
| 3 |
| 2 |
| 3 |
| 2 |
| b |
| x |
| 2 |
| x |
| 2 |
| π |
| 2 |
| 3 |
| 2 |
(1)求|
| a |
| b |
(2)求函数f(x)=
| a |
| b |
| a |
| b |
(1)∵x∈[
,
π],∴-1≤cos2x≤1,
∴|
+
|=
=
.
∴0≤|
+
|≤2. (4分)
(2)∵x∈[
,
π],∴-1≤cosx≤0. …(6分)
∵f(x)=
•
-|
+
|=cos2x-
=2cos2x-1-
=2cos2x+2cosx-1,…(10分)
∴当cosx=-
,即x=
π或x=
π时,f(x)=
•
-|
+
|取最小值-
.…(12分)
| π |
| 2 |
| 3 |
| 2 |
∴|
| a |
| b |
(cos
|
| 2+2cos2x |
∴0≤|
| a |
| b |
(2)∵x∈[
| π |
| 2 |
| 3 |
| 2 |
∵f(x)=
| a |
| b |
| a |
| b |
| 2+2cos2x |
| 4cos2x |
∴当cosx=-
| 1 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| a |
| b |
| a |
| b |
| 3 |
| 2 |

练习册系列答案
相关题目
 的周长是6,中心角是1弧度,则该扇形的面积为________.
的周长是6,中心角是1弧度,则该扇形的面积为________.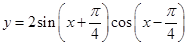 和直线
和直线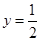 在y轴右侧的交点按横坐标从小到大依次记为P1、P2、P3…,则|P2P4|等于______________。
在y轴右侧的交点按横坐标从小到大依次记为P1、P2、P3…,则|P2P4|等于______________。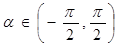 ,求使sin
,求使sin 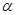 =
=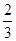 成立的
成立的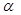 =
=