题目内容
【题目】已知函数f（x）
与g（x）＝3elnx+mx的图象有4个不同的交点，则实数m的取值范围是（ ）
A.（﹣3，
）B.（﹣1，）C.（﹣1，3）D.（0，3）
【答案】B
【解析】
由题意可得m＝
﹣
（x＞0且x≠e）有4个不等实根，设h（x）＝﹣，进而求导和极值点，最值，考虑x→+∞，
→0可得h（x）的极限，即可得到所求m的范围；
函数
与
的图象有4个不同的交点，即为
，（x＞0且x≠e）有4个不等实根，
设
，
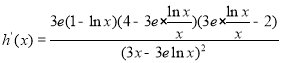
由
的导数为：
，
当x>e时，y′<0，函数y单调递减，
当0<x<e时，y′>0，函数y单调递增，
可得x＝e处取得极大值，且为
，因此
，所以
，而当
时，
.
，即2x＝3elnx有两解，设为
，且
，
，
显然当
时，
单调递减
当
时，
单调递增
当
时，单调递减
当
时，单调递增，
由x→+∞，→0，可得﹣＝
，→
，
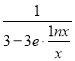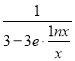所以要想函数与的图象有4个不同的交点，只需
.
故选：B
练习册系列答案
相关题目
