��Ŀ����
7����ƽ��ֱ������ϵ�л������ж�Ԫһ�β���ʽ��Ľ�����ʾ��������1��$\left\{\begin{array}{l}{x��2}\\{y��2x-3}\end{array}\right.$��
��2��$\left\{\begin{array}{l}{2x+y��4}\\{x��0}\\{y��0}\end{array}\right.$��
��3��$\left\{\begin{array}{l}{-1��x��5}\\{-2��y��3}\\{x+y��6}\end{array}\right.$��
���� ���ݶ�Ԫһ�β���ʽ���ʾƽ�����������ͼ���ɣ�
��� �⣺��1��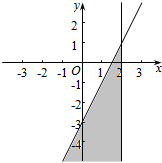 ��2��
��2�� ��3��
��3��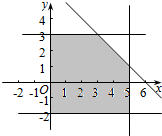
���� ������Ҫ�����Ԫһ�β���ʽ���ʾƽ�����Ƚϻ�����

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
15����֪����{an}����a1=1��a2=2����$\frac{{a}_{n-1}-{a}_{n}}{{a}_{n-1}}$=$\frac{{a}_{n}-{a}_{n+1}}{{a}_{n}}$��n��2����������{an}��ǰ4��͵��ڣ�������
| A�� | 18 | B�� | 8 | C�� | 15 | D�� | 17 |
12��һ�������������ͼ��ͼ��ʾ�����������ǣ�������


| A�� | $\frac{7��}{6}$ | B�� | $\frac{5��}{6}$ | C�� | $\frac{5��}{3}$ | D�� | $\frac{4��}{3}$ |
19����f��x��=$\frac{{e}^{|x|}+x+1}{{e}^{|x|}+1}$������[-m��m]��m��0���ϵ����ֵΪp����СֵΪq����p+q=��������
| A�� | 4 | B�� | 3.5 | C�� | 3 | D�� | 2 |
16����֪˫����$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0���Ľ�������ʵ��ļн�Ϊ30�㣬��˫���ߵ�������Ϊ��������
| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | $\frac{2\sqrt{3}}{3}$ | D�� | 2 |