题目内容
13.求下列各式的值.(Ⅰ)设${x}^{\frac{1}{2}}+{x}^{{-}^{\frac{1}{2}}}=3$,求x+x-1;
(Ⅱ)(lg2)2+lg5•lg20+($\root{3}{2}×\sqrt{3})^{6}+(2\frac{1}{4})^{\frac{1}{2}}-0.{3}^{0}-1{6}^{-\frac{3}{4}}$6+$(2\frac{1}{4})^{\frac{1}{2}}$-0.30-$1{6}^{{-}^{\frac{3}{4}}}$.
分析 (Ⅰ)利用x+x-1=$({x}^{\frac{1}{2}}+{x}^{-\frac{1}{2}})^{2}$-2即可得出.
(Ⅱ)利用指数与对数的运算法则即可得出.
解答 解:(Ⅰ)∵${x}^{\frac{1}{2}}+{x}^{{-}^{\frac{1}{2}}}=3$,
∴x+x-1=$({x}^{\frac{1}{2}}+{x}^{-\frac{1}{2}})^{2}$-2=32-2=7.
(Ⅱ)原式=(lg2)2+lg5(1+lg2)+22×33+$(\frac{3}{2})^{2×\frac{1}{2}}$-1-${2}^{4×(-\frac{3}{4})}$
=lg2(lg2+lg5)+lg5+108+$\frac{3}{2}$-1-$\frac{1}{8}$
=lg2+lg5+108+$\frac{3}{8}$
=109+$\frac{3}{8}$
=$109\frac{3}{8}$.
点评 本题考查了指数与对数的运算法则、乘法公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.已知数列{an}为等比数列,Sn是它的前n项和,若a2•a3=2a1,且a4与2a7的等差中项为$\frac{5}{4}$,则S6=( )
| A. | 35 | B. | 33 | C. | 31 | D. | $\frac{63}{2}$ |
2.已知a=log32,b=log30.5,c=1.10.5,那么a、b、c的大小关系为( )
| A. | b>c>a | B. | b>a>c | C. | a>b>c | D. | c>a>b |
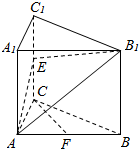 已知直棱柱ABC-A1B1C1,∠ACB=60°,AC=BC=4,AA1=6,E、F分别是棱CC1、AB的中点.
已知直棱柱ABC-A1B1C1,∠ACB=60°,AC=BC=4,AA1=6,E、F分别是棱CC1、AB的中点.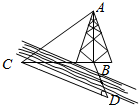 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在C测得塔顶A的仰角为60°,则塔的高度为15$\sqrt{6}$m.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在C测得塔顶A的仰角为60°,则塔的高度为15$\sqrt{6}$m.