题目内容
已知定义在(0,+∞)上的两个函数f(x)=x2-alnx,g(x)=x-a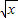 ,且f(x)在x=1处取得极值.
,且f(x)在x=1处取得极值.(1)求a的值及函数g(x)的单调区间;
(2)把g(x)对应的曲线向上平移6个单位后得曲线C1,求C1与f(x)对应曲线C2的交点个数,并说明理由.
【答案】分析:(1)先根据f'(1)=0求出a的值,然后求出g′(x),最后解g′(x)>0与g′(x)<0,即可求出函数g(x)的单调区间;
(2)由题意知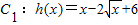 ,问题转化为
,问题转化为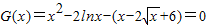 在(0,+∞)上解的个数,然后利用导数研究函数的单调性,从而可判定解的个数.
在(0,+∞)上解的个数,然后利用导数研究函数的单调性,从而可判定解的个数.
解答:(Ⅰ)∵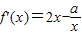 ,
,
∴f'(1)=2-a=0,∴a=2
∴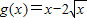 .
.
由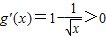 ,得x>1;由
,得x>1;由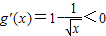 ,得0<x<1.
,得0<x<1.
∴g(x)的单调递减区间是(0,1),单调递增区间是(1,+∞).(5分)
(3)由题意知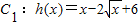 .
.
问题转化为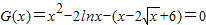 在(0,+∞)上解的个数
在(0,+∞)上解的个数
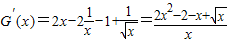 =
=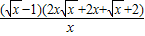 .
.
由G'(x)>0,得x>1;由G'(x)<0,得0<x<1.
∴G(x)在区间(1,+∞)上单调递增,在区间(0,1)上单调递减.
又G(1)=-4<0,所以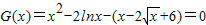 在(0,+∞)上有2个解.
在(0,+∞)上有2个解.
即C1与f(x)对应曲线C2的交点个数是2.(12分)
点评:本题主要考查了利用导数研究函数的极值,以及函数的单调性和图象交点问题,同时考查了转化的思想,属于中档题.
(2)由题意知
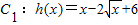 ,问题转化为
,问题转化为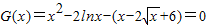 在(0,+∞)上解的个数,然后利用导数研究函数的单调性,从而可判定解的个数.
在(0,+∞)上解的个数,然后利用导数研究函数的单调性,从而可判定解的个数.解答:(Ⅰ)∵
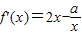 ,
,∴f'(1)=2-a=0,∴a=2
∴
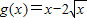 .
.由
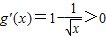 ,得x>1;由
,得x>1;由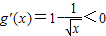 ,得0<x<1.
,得0<x<1.∴g(x)的单调递减区间是(0,1),单调递增区间是(1,+∞).(5分)
(3)由题意知
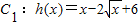 .
.问题转化为
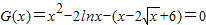 在(0,+∞)上解的个数
在(0,+∞)上解的个数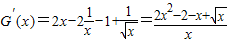 =
=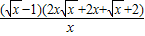 .
.由G'(x)>0,得x>1;由G'(x)<0,得0<x<1.
∴G(x)在区间(1,+∞)上单调递增,在区间(0,1)上单调递减.
又G(1)=-4<0,所以
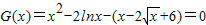 在(0,+∞)上有2个解.
在(0,+∞)上有2个解.即C1与f(x)对应曲线C2的交点个数是2.(12分)
点评:本题主要考查了利用导数研究函数的极值,以及函数的单调性和图象交点问题,同时考查了转化的思想,属于中档题.

练习册系列答案
相关题目
 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论: