题目内容
设椭圆![]() 的两个焦点是
的两个焦点是![]()
(1)设E是直线![]() 与椭圆的一个公共点,求使得
与椭圆的一个公共点,求使得![]() 取最小值时椭圆的方程;
取最小值时椭圆的方程;
(2)已知![]() 设斜率为
设斜率为![]() 的直线
的直线![]() 与条件(1)下的椭圆交于不同的两点A,B,点Q满足
与条件(1)下的椭圆交于不同的两点A,B,点Q满足![]() ,且
,且![]() ,求直线
,求直线![]() 在
在![]() 轴上截距的取值范围。
轴上截距的取值范围。
解:(1)由题意,知![]()
由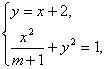
得![]()
由![]()
解得![]() (舍去)
(舍去)
![]() 3分
3分
此时![]()
当且仅当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,
,
此时椭圆方程为![]() 4分
4分
(2)设直线![]() 的方程为
的方程为![]()
由方程组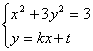 ,
,
消去![]() 得
得![]()
![]() 直线
直线![]() 与椭圆交于不同两点A、B
与椭圆交于不同两点A、B
![]()
即![]() ① 6分
① 6分
设![]() ,
,
则![]()
由![]() ,得Q为线段AB的中点,
,得Q为线段AB的中点,
则![]() 8分
8分
![]()
![]() ,
,
即
化简得![]()
代入①得![]() 10分
10分
解得![]() 11分
11分
又由![]()
所以,直线![]() 在
在![]() 轴上的截距
轴上的截距![]() 的取值范围是
的取值范围是![]() 12分
12分

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
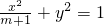 的两个焦点是F1(-c,0),F2(c,0)(c>0).
的两个焦点是F1(-c,0),F2(c,0)(c>0).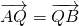 ,且
,且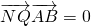 ,求直线l在y轴上截距的取值范围.
,求直线l在y轴上截距的取值范围.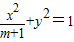 的两个焦点是F1(-c,0),F2(c,0)(c>0).
的两个焦点是F1(-c,0),F2(c,0)(c>0).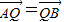 ,且
,且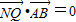 ,求直线l在y轴上截距的取值范围.
,求直线l在y轴上截距的取值范围. 的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C上的点到焦点F2的最短距离为
的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C上的点到焦点F2的最短距离为 .
.