Question

（04年全国卷III文）(12分)

设椭圆的两个焦点是 F₁(-c,0), F₂(c,0)(c>0)，且椭圆上存在点P，使得直线 PF₁与直线PF₂垂直．

(I)求实数 m 的取值范围．

(II)设l是相应于焦点 F₂的准线，直线PF₂与l相交于点Q. 若，求直线PF₂的方程．

Answer 1

解析：⑴∵直线PF₁⊥直线PF₂　

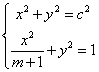∴以O为圆心以c为半径的圆：x²+y²=c²与椭圆：有交点.即有解

又∵c²=a²-b²=m+1-1=m>0　

∴　∴

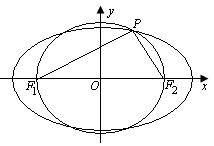
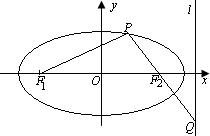
⑵设P(x,y), 直线PF₂方程为：y=k(x-c)

∵直线l的方程为：

∴点Q的坐标为()

∵  ∴点P分有向线段所成比为

∵F₂(,0),Q ()  ∴P()

∵点P在椭圆上　∴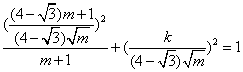

∴

直线PF₂的方程为：y=(x-).