题目内容
设a≥0,函数f(x)=[x2+(a-3)x-2a+3]ex,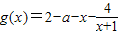 .
.( I)当a≥1时,求f(x)的最小值;
( II)假设存在x1,x2∈(0,+∞),使得|f(x1)-g(x2)|<1成立,求a的取值范围.
【答案】分析:( I)求出f(x)的导数,利用导数求出函数的最值问题;
( II)根据第一问已经知道f(x)的值域,需要分两种情况:a>1或0<a<1,根据|f(x1)-g(x2)|<1求出a的范围;
解答:解:(Ⅰ)∵f'(x)=[x2+(a-1)x-a]ex=(x+a)(x-1)ex
∵a≥1,
∴x∈(-∞,-a)时,f(x)递增,x∈(-a,1)时,f(x)递减,x∈(1,+∞)时,f(x)递增,
所以f(x)的极大值点为x1=-a,极小值点为x2=1,
而f(1)=(1-a)e≤0,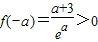 ,
,
由于,对二次函数y=x2+(a-3)x-2a+3,对称轴为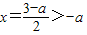 ,y(-a)=a+3>0,
,y(-a)=a+3>0,
∴当x≤-a时,y=x2+(a-3)x-2a+3>0,
∴f(x)>0.
当x>-a时,f(x)的最小值为f(1)=(1-a)e.
所以,f(x)的最小值是(1-a)e.
( II)由(Ⅰ)知f(x)在(0,+∞)的值域是:
当a≥1时,为[(1-a)e,+∞),当0<a<1时,为(0,+∞).
而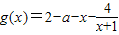 在(0,+∞)的值域是为(-∞,-a-1),
在(0,+∞)的值域是为(-∞,-a-1),
所以,当a≥1时,令(1-a)e-(-a-1)<1,并解得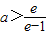 ,
,
当0<a<1时,令0-(-a-1)<1,无解.
因此,a的取值范围是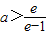 .
.
点评:此题考查利用导数研究函数的单调性,比较简单,但是第二问涉及恒成立的问题,就比较复杂,考查了分类讨论思想的应用,关于导数求最值的应用在高考是一个热点问题,每年都会考一道大题,难度中等;
( II)根据第一问已经知道f(x)的值域,需要分两种情况:a>1或0<a<1,根据|f(x1)-g(x2)|<1求出a的范围;
解答:解:(Ⅰ)∵f'(x)=[x2+(a-1)x-a]ex=(x+a)(x-1)ex
∵a≥1,
∴x∈(-∞,-a)时,f(x)递增,x∈(-a,1)时,f(x)递减,x∈(1,+∞)时,f(x)递增,
所以f(x)的极大值点为x1=-a,极小值点为x2=1,
而f(1)=(1-a)e≤0,
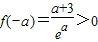 ,
,由于,对二次函数y=x2+(a-3)x-2a+3,对称轴为
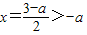 ,y(-a)=a+3>0,
,y(-a)=a+3>0,∴当x≤-a时,y=x2+(a-3)x-2a+3>0,
∴f(x)>0.
当x>-a时,f(x)的最小值为f(1)=(1-a)e.
所以,f(x)的最小值是(1-a)e.
( II)由(Ⅰ)知f(x)在(0,+∞)的值域是:
当a≥1时,为[(1-a)e,+∞),当0<a<1时,为(0,+∞).
而
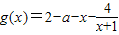 在(0,+∞)的值域是为(-∞,-a-1),
在(0,+∞)的值域是为(-∞,-a-1),所以,当a≥1时,令(1-a)e-(-a-1)<1,并解得
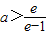 ,
,当0<a<1时,令0-(-a-1)<1,无解.
因此,a的取值范围是
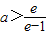 .
.点评:此题考查利用导数研究函数的单调性,比较简单,但是第二问涉及恒成立的问题,就比较复杂,考查了分类讨论思想的应用,关于导数求最值的应用在高考是一个热点问题,每年都会考一道大题,难度中等;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目