Question

【题目】已知四棱锥的底面为等腰梯形, , 垂足为是四棱锥的高,为中点,设

（1）证明：；

（2）若，求直线与平面所成角的正弦值．

Answer 1

【答案】（1）证明见解析；（2）.

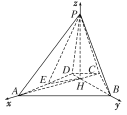
【解析】分析：（1）以H为原点，HA，HB，HP所在直线分别为x，y，z轴，建立空间直角坐标系，利用向量法证明·＝0即得PE⊥BC.（2）利用线面角的向量公式求直线与平面所成角的正弦值．

详解：以H为原点，HA，HB，HP所在直线分别为x，y，z轴，建立空间直角坐标系如图，则A(1,0,0)，B(0,1,0)．

(1)证明：设C(m,0,0)，P(0,0，n)(m<0，n>0)，则D(0，m,0)，E(， ，0)．

可得＝(， ，－n)，＝(m，－1,0)． 因为·＝- ＋0＝0，

所以PE⊥BC.

(2)由已知条件可得m＝－，n＝1，

故C(－，0,0)，D(0，－，0)，E(，－，0)，

P(0，0,1)．设n＝(x，y，z)为平面PEH的法向量，

则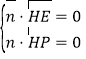，即，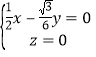

因此可以取n＝(1，，0)．

由＝(1,0，－1)，可得|cos〈，n〉|＝，

所以直线PA与平面PEH所成角的正弦值为.