题目内容
已知曲线C上的动点P( )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
(1)求曲线C的方程。
(2)过点M(1,2)的直线 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线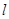 的方程。
的方程。
(1)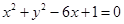 (或
(或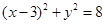 )(2)
)(2)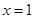 或
或 .
.
解析试题分析:(1)根据动点P(x,y)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为 ,建立方程,化简可得曲线C的方程.
,建立方程,化简可得曲线C的方程.
(2)分类讨论,设出直线方程,求出圆心到直线的距离,利用勾股定理,即可求得直线l的方程.
试题解析:(1)由题意得|PA|= |PB| 2分;
|PB| 2分;
故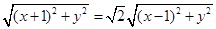 3分;
3分;
化简得: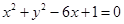 (或
(或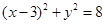 )即为所求。 5分;
)即为所求。 5分;
(2)当直线 的斜率不存在时,直线
的斜率不存在时,直线 的方程为
的方程为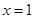 ,
,
将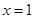 代入方程
代入方程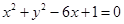 得
得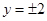 ,所以|MN|=4,满足题意。 8分;
,所以|MN|=4,满足题意。 8分;
当直线 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为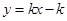 +2
+2
由圆心到直线的距离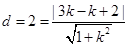 10分;
10分;
解得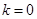 ,此时直线
,此时直线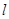 的方程为
的方程为
综上所述,满足题意的直线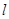 的方程为:
的方程为: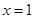 或
或 。 12分.
。 12分.
考点:直线和圆的方程的应用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
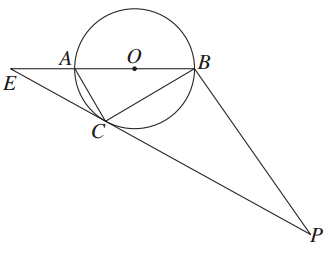
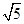 ,求PB的长.
,求PB的长.

 ,求直线MQ的方程.
,求直线MQ的方程. 中,如图,已知椭圆E:
中,如图,已知椭圆E: 的左、右顶点分别为
的左、右顶点分别为 、
、 ,上、下顶点分别为
,上、下顶点分别为 、
、 .设直线
.设直线 的倾斜角的正弦值为
的倾斜角的正弦值为 ,圆
,圆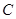 与以线段
与以线段 为直径的圆关于直线
为直径的圆关于直线
 ,求圆
,求圆 中,已知点
中,已知点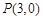 在圆
在圆 内,动直线
内,动直线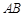 过点
过点 且交圆
且交圆 于
于 两点,若△ABC的面积的最大值为
两点,若△ABC的面积的最大值为 ,则实数
,则实数 的取值范围为 .
的取值范围为 . 为圆心的圆经过点
为圆心的圆经过点 和
和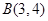 ,且圆心在直线
,且圆心在直线 上.
上. 在圆
在圆 的面积的最大值.
的面积的最大值. 、
、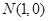 ,点
,点 为坐标平面内的动点,满足
为坐标平面内的动点,满足 .
. 是动点
是动点 是
是 轴上的一动点,试讨论直线
轴上的一动点,试讨论直线 与圆
与圆 的位置关系.
的位置关系. ,则
,则 的大小为 .
的大小为 .