题目内容
已知圆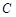 过点
过点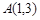 ,
,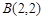 ,并且直线
,并且直线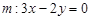 平分圆的面积.
平分圆的面积.
(1)求圆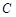 的方程;
的方程;
(2)若过点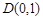 ,且斜率为
,且斜率为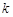 的直线
的直线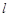 与圆
与圆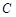 有两个不同的公共点
有两个不同的公共点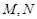 .
.
①求实数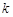 的取值范围; ②若
的取值范围; ②若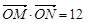 ,求
,求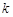 的值.
的值.
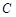 过点
过点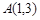 ,
,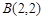 ,并且直线
,并且直线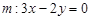 平分圆的面积.
平分圆的面积.(1)求圆
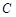 的方程;
的方程;(2)若过点
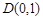 ,且斜率为
,且斜率为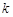 的直线
的直线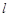 与圆
与圆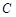 有两个不同的公共点
有两个不同的公共点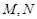 .
.①求实数
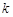 的取值范围; ②若
的取值范围; ②若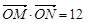 ,求
,求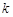 的值.
的值.(1)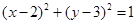 ;(2)①:实数
;(2)①:实数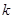 的取值范围是
的取值范围是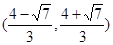 ,②:
,②: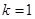 .
.
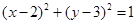 ;(2)①:实数
;(2)①:实数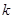 的取值范围是
的取值范围是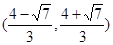 ,②:
,②: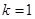 .
.试题分析:(1)由题意直线
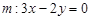 平分圆的面积可知圆心
平分圆的面积可知圆心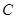 在直线上,因此可将
在直线上,因此可将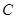 的坐标设为
的坐标设为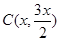 ,再由圆
,再由圆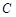 过点
过点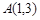 ,
,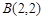 可知
可知 ,即可得到关于
,即可得到关于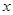 的方程:
的方程: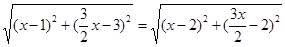 ,解得
,解得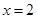 ,即有圆心坐标
,即有圆心坐标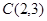 ,半径
,半径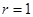 ,从而可知圆的方程为
,从而可知圆的方程为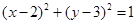 ;(2)①:根据题意可设直线
;(2)①:根据题意可设直线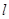 的方程为
的方程为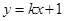 ,代入圆方程并化简可得
,代入圆方程并化简可得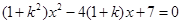 ,从而直线与圆有两个不同的交点
,从而直线与圆有两个不同的交点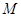 ,
,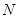 等价于方程有两个不想等的实数根,从而
等价于方程有两个不想等的实数根,从而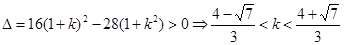 ,②:由题意可知若设设
,②:由题意可知若设设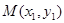 ,
,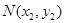 ,则
,则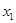 ,
,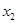 为方程
为方程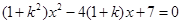 的两根,从而
的两根,从而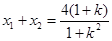 ,
,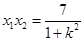 ,
,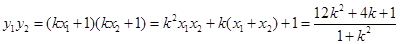 ,因此可以由
,因此可以由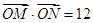 得到关于
得到关于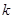 的方程:
的方程: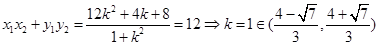 ,即
,即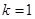 .
.试题解析:(1)∵
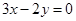 平分圆的面积,∴圆心
平分圆的面积,∴圆心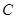 在直线上,∴设
在直线上,∴设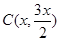 ,又∵圆
,又∵圆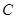 过点
过点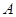 ,
,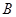 ,
,∴
 ,即
,即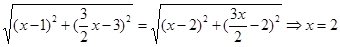 ,∴
,∴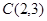 ,半径
,半径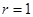 ,
,∴圆
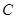 的方程为
的方程为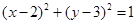 ; 4分;
; 4分;①:设直线
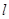 的方程为
的方程为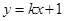 ,代入
,代入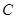 并化简可得:
并化简可得: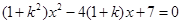 ,
,∵直线
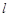 与圆
与圆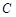 有两个不同的公共点
有两个不同的公共点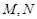 ,∴
,∴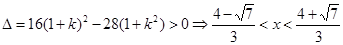 ,
,即实数
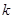 的取值范围是
的取值范围是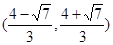 , 4分
, 4分②:设
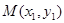 ,
,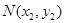 ,由①可知
,由①可知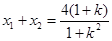 ,
,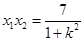 ,
,∴
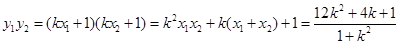 ,
,∴
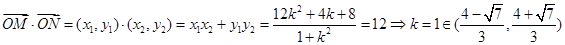 ,
,∴
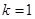 . 4分
. 4分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
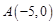 ,
,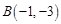 ,若圆
,若圆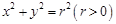 上恰有两点
上恰有两点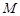 ,
,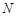 ,使得
,使得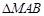 和
和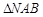 的面积均为
的面积均为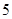 ,则
,则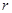 的取值范围是 .
的取值范围是 .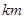 的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?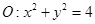 和圆
和圆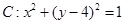 .
.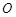 和圆
和圆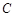 的位置关系;
的位置关系;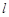 ,求切线
,求切线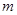 交圆
交圆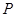 ,使得圆
,使得圆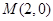 ?若存在,求出圆
?若存在,求出圆 (
( )
) 时,求经过原点且与圆
时,求经过原点且与圆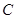 相切的直线
相切的直线 的方程;
的方程;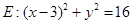 的内部,求实数
的内部,求实数 的取值范围.
的取值范围.