题目内容
【题目】正方体
的棱长为2，E，F，G分别为
，
，
的中点，则（ ）
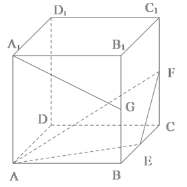
A.直线
与直线
垂直
B.直线
与平面
不平行
C.平面截正方体所得的截面面积为
D.点C与点G到平面的距离相等
【答案】C
【解析】
根据条件对选项进行逐一分析, A.若有
，则能得到
平面
，进一步得到
，显然不成立，可判断. B.取
的中点Q，连接
，
,可得平面
平面，从而可判断. C.连接
，
，延长，
交于点S，由条件可得
，截面即为梯形
，再计算其面积. D.用等体积法分别求出点C和点G到平面的距离，从而判断.
A.若，
又因为
且
，所以平面，
所以
，所以，显然不成立，故结论错误；
B.如图所示，取的中点Q，连接，，
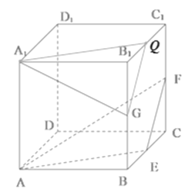
由条件可知：
，
，且
，
，
所以平面平面，
又因为
平面
，所以
平面，故结论不正确；
C.如图所示，连接，，延长，交于点S,
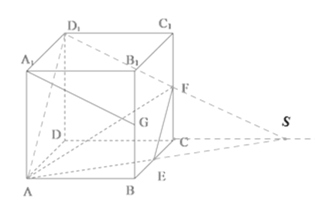
因为E，F为
，
的中点，所以，所以A，E，F，
四点共面，
所以，截面即为梯形
又因为
，
，
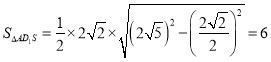所以
，所以
，故结论正确；
D.记点C与点G到平面的距离分别为
，
，
因为
.
又因为
，
所以
，故结论错误.
故选C.
练习册系列答案
优学名师名题系列答案
相关题目
【题目】某市农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月4日的每天昼夜温度与实验室每天每100颗种子中的发芽数，得到如下数据：
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 |
温差 | 11 | 13 | 12 | 8 |
发芽数（颗） | 26 | 32 | 26 | 17 |
根据表中12月1日至12月3日的数据，求得线性回归方程
中的
，则求得的
_____；若用12月4日的数据进行检验，检验方法如下：先用求得的线性回归方程计算发芽数
，再求与实际发芽数
的差，若差值的绝对值不超过2颗，则认为得到的线性回归方程是可靠的，则求得的线性回归方程_____（填“可靠”或“不可靠”）．
