题目内容
根据二次函数的性质填空:
(1)一般式:y=ax2+bx+c(a≠0);对称轴方程是________;顶点为________;
(2)两点式:y=a(x-x1)(x-x2);对称轴方程是________;与x轴的交点为________;
(3)顶点式:y=a(x-k)2+h;对称轴方程是________;顶点为________.
解:(1)一般式:y=ax2+bx+c(a≠0)=a 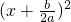 +
+ ,
,
故对称轴方程是x=- ,顶点为(-
,顶点为(- ,
, ),
),
(2)两点式:y=a(x-x1)(x-x2)=a(x2-(x1+x2 )x+x1x2 )=a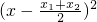 -a
-a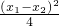 ;
;
对称轴方程是 x= ,与x轴的交点为 (x1,0)、(x2,0),
,与x轴的交点为 (x1,0)、(x2,0),
(3)顶点式:y=a(x-k)2+h;对称轴方程是 x=k,顶点为 (k,h ),
综上,故答案为 (1)x=- ,(-
,(- ,
, ); (2)x=
); (2)x= ,(x1,0)、(x2,0);(3)x=k,(k,h ).
,(x1,0)、(x2,0);(3)x=k,(k,h ).
分析:(1)把一般式通过配方,可得到二次函数的对称轴及顶点坐标;
(2)对于二次函数的两点式,可以直接得到图象与x轴的交点,对称轴是图象与x轴的交点构成的线段的中垂线.
(3)由二次函数的顶点式可直接得到对称轴方程和定点的坐标.
点评:本题考查二次函数的性质的应用,以及二次函数的几种形式.
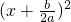 +
+ ,
,故对称轴方程是x=-
 ,顶点为(-
,顶点为(- ,
, ),
),(2)两点式:y=a(x-x1)(x-x2)=a(x2-(x1+x2 )x+x1x2 )=a
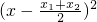 -a
-a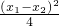 ;
;对称轴方程是 x=
 ,与x轴的交点为 (x1,0)、(x2,0),
,与x轴的交点为 (x1,0)、(x2,0),(3)顶点式:y=a(x-k)2+h;对称轴方程是 x=k,顶点为 (k,h ),
综上,故答案为 (1)x=-
 ,(-
,(- ,
, ); (2)x=
); (2)x= ,(x1,0)、(x2,0);(3)x=k,(k,h ).
,(x1,0)、(x2,0);(3)x=k,(k,h ).分析:(1)把一般式通过配方,可得到二次函数的对称轴及顶点坐标;
(2)对于二次函数的两点式,可以直接得到图象与x轴的交点,对称轴是图象与x轴的交点构成的线段的中垂线.
(3)由二次函数的顶点式可直接得到对称轴方程和定点的坐标.
点评:本题考查二次函数的性质的应用,以及二次函数的几种形式.

练习册系列答案
相关题目
 已知二次函数y=-x2+4x+5
已知二次函数y=-x2+4x+5
 的图象上有
的图象上有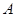 、
、 、
、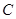 三点,横坐标分别为
三点,横坐标分别为 其中
其中 .
.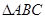 的面积
的面积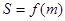 的表达式;
的表达式;