题目内容
 已知二次函数y=-x2+4x+5
已知二次函数y=-x2+4x+5(1)配成顶点式:y=-x2+4x+5=-(…)2+(…)
(2)画出二次函数y=-x2+4x+5的图象
(3)根据二次函数的图象写出-x2+4x+5≥0的解集
{x|-1≤x≤5}
{x|-1≤x≤5}
根据二次函数的图象写出-x2+4x+5<0的解集{x|x<-1或x>5}
{x|x<-1或x>5}
.分析:(1)用配方法求得顶点式,从而得出答案.
(2)利用(1)得出的顶点式,列表,描点,连线作出图形即可;
(2)写出函数图象在x轴上方的部分的x的取值范围即可得-x2+4x+5≥0的解集;写出函数图象在x轴下方的部分的x的取值范围即可得-x2+4x+5<0的解集.
(2)利用(1)得出的顶点式,列表,描点,连线作出图形即可;
(2)写出函数图象在x轴上方的部分的x的取值范围即可得-x2+4x+5≥0的解集;写出函数图象在x轴下方的部分的x的取值范围即可得-x2+4x+5<0的解集.
解答: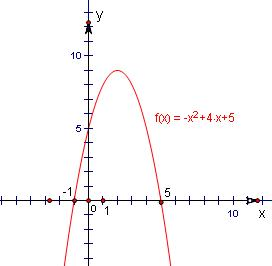 解:(1)配成顶点式:y=-x2+4x+5=-(.x-2.)2+(..9…)(3分)
解:(1)配成顶点式:y=-x2+4x+5=-(.x-2.)2+(..9…)(3分)
(2)画出二次函数y=-x2+4x+5的图象
如图所示. (8分)
(3)根据二次函数的图象写出-x2+4x+5≥0的解集{x|-1≤x≤5}(10分)
根据二次函数的图象写出-x2+4x+5<0的解集{x|x<-1或x>5}(12分)
 解:(1)配成顶点式:y=-x2+4x+5=-(.x-2.)2+(..9…)(3分)
解:(1)配成顶点式:y=-x2+4x+5=-(.x-2.)2+(..9…)(3分)(2)画出二次函数y=-x2+4x+5的图象
如图所示. (8分)
(3)根据二次函数的图象写出-x2+4x+5≥0的解集{x|-1≤x≤5}(10分)
根据二次函数的图象写出-x2+4x+5<0的解集{x|x<-1或x>5}(12分)
点评:本题考查了二次函数图象,二次函数的性质,一元二次不等式的解法,利用顶点坐标的变化确定函数解析式是此类题目常用的方法,要熟练掌握并灵活运用.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 如图所示,已知二次函数y=-x2+9,矩形ABOC的顶点A在第一象限内,且A在抛物线上,顶点B、C分别在y轴、x轴上,设点A的坐标为(x,y).
如图所示,已知二次函数y=-x2+9,矩形ABOC的顶点A在第一象限内,且A在抛物线上,顶点B、C分别在y轴、x轴上,设点A的坐标为(x,y).