题目内容
设函数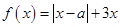 ,其中
,其中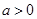 .
.
(Ⅰ)当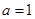 时,求不等式
时,求不等式 的解集;
的解集;
(Ⅱ)若不等式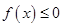 的解集为
的解集为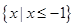 ,求
,求 的值.
的值.
(Ⅰ)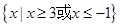 . (Ⅱ)
. (Ⅱ) 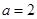 。
。
解析试题分析:(Ⅰ)当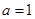 时,
时,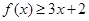 可化为
可化为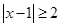 .由此可得
.由此可得 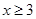 或
或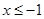 .
.
故不等式 的解集为
的解集为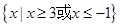 . 5分
. 5分
(Ⅱ) 由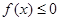 得
得 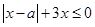
此不等式化为不等式组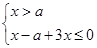 或
或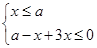
即 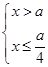 或
或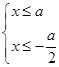
因为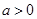 ,所以不等式组的解集为
,所以不等式组的解集为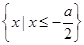
由题设可得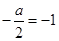 ,故
,故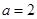 . 10分
. 10分
考点:本题主要考查绝对值不等式的解法,简单不等式组的解法。
点评:中档题,利用转化思想,将含绝对值不等式转化成不等式组,是解答这类题目的一般方法,往往涉及分类讨论思想的应用。

练习册系列答案
相关题目
 定义在
定义在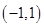 上,对于任意的
上,对于任意的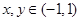 ,有
,有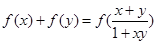 ,且当
,且当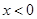 时,
时,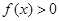 .
.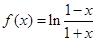 是否满足这些条件;
是否满足这些条件;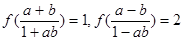 ,且
,且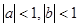 ,求
,求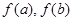 的值.
的值.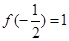 ,试解关于
,试解关于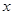 的方程
的方程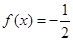 .
.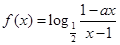 为奇函数,
为奇函数, 为常数.
为常数. 在区间(1,+∞)内的单调性,并证明你的判断正确;
在区间(1,+∞)内的单调性,并证明你的判断正确;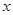 的值,不等式
的值,不等式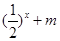 恒成立,求实数
恒成立,求实数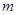 的取值范围.
的取值范围.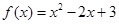
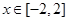 时,求
时,求 的值域
的值域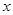 的不等式:
的不等式: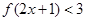
 的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
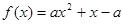
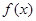 有最 大值
有最 大值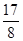 ,求实数
,求实数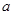 的值
的值
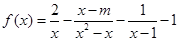
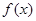 无零点,求实数
无零点,求实数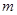 的取值范围;
的取值范围;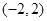 有且仅有一个零点,求实数
有且仅有一个零点,求实数 ,满足
,满足 ;
; 有唯一的解;求实数
有唯一的解;求实数 的值;
的值; 在区间
在区间 上不是单调函数,求实数
上不是单调函数,求实数 的取值范围。
的取值范围。