题目内容
18.已知数列{an}满足a1=1,(2n-1)an+1=2(2n+1)an,则a6=352.分析 根据数列的递推公式,利用累积法即可得到结论.
解答 解:由(2n-1)an+1=2(2n+1)an,得
$\frac{{a}_{n+1}}{{a}_{n}}=\frac{2(2n+1)}{2n-1}$,
∴$\frac{{a}_{2}}{{a}_{1}}=\frac{2×3}{1}$,$\frac{{a}_{3}}{{a}_{2}}=\frac{2×5}{3}$,
…
$\frac{{a}_{6}}{{a}_{5}}=\frac{2×11}{9}$,
则${a}_{6}=\frac{{a}_{2}}{{a}_{1}}•\frac{{a}_{3}}{{a}_{2}}…\frac{{a}_{6}}{{a}_{5}}$=$\frac{2×3}{1}×\frac{2×5}{3}×…×\frac{2×11}{9}$=25×11=352.
故答案为:352.
点评 本题主要考查数列的递推公式的应用,利用累积法是解决本题的关键,考查学生的计算能力,是中档题.

练习册系列答案
相关题目
6.已知f(x)=ax2+bx+c,(a>0),若f(-1)=f(3),则f(-1),f(1),f(4)的大小关系为 ( )
| A. | f(-1)<f(1)<f(4) | B. | f(1)<f(-1)<f(4) | C. | f(-1)<f(4)<f(1) | D. | f(4)<f(-1)<f(1) |
10.已知全集U=R,集合A={x|2<x≤3},集合B={x|2≤x≤4},则(∁UA)∩B等于( )
| A. | {x|3≤x≤4} | B. | {x|3<x≤4} | C. | {x|x=2或3<x≤4} | D. | {x|3<x<4} |
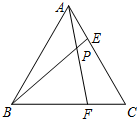 等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.