题目内容
(2012•江西)在直角三角形ABC中,点D是斜边AB的中点,点P为线段CD的中点,则
=( )
| |PA|2+|PB|2 |
| |PC|2 |
分析:以D为原点,AB所在直线为x轴,建立坐标系,由题意得以AB为直径的圆必定经过C点,因此设AB=2r,∠CDB=α,得到A、B、C和P各点的坐标,运用两点的距离公式求出|PA|2+|PB|2和|PC|2的值,即可求出
的值.
| |PA|2+|PB|2 |
| |PC|2 |
解答:解: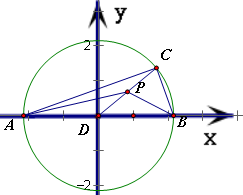 以D为原点,AB所在直线为x轴,建立如图坐标系,
以D为原点,AB所在直线为x轴,建立如图坐标系,
∵AB是Rt△ABC的斜边,
∴以AB为直径的圆必定经过C点
设AB=2r,∠CDB=α,则
A(-r,0),B(r,0),C(rcosα,rsinα)
∵点P为线段CD的中点,
∴P(
rcosα,
rsinα)
∴|PA|2=(
rcosα+r)2+(
rsinα)2=
r2+r2cosα,
|PB|2=(
rcosα-r)2+(
rsinα)2=
r2-r2cosα,
可得|PA|2+|PB|2=
r2
又∵点P为线段CD的中点,CD=r
∴|PC|2=(
r)2=
r2
所以:
=
=10
故选D
 以D为原点,AB所在直线为x轴,建立如图坐标系,
以D为原点,AB所在直线为x轴,建立如图坐标系,∵AB是Rt△ABC的斜边,
∴以AB为直径的圆必定经过C点
设AB=2r,∠CDB=α,则
A(-r,0),B(r,0),C(rcosα,rsinα)
∵点P为线段CD的中点,
∴P(
| 1 |
| 2 |
| 1 |
| 2 |
∴|PA|2=(
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
|PB|2=(
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
可得|PA|2+|PB|2=
| 5 |
| 2 |
又∵点P为线段CD的中点,CD=r
∴|PC|2=(
| 1 |
| 2 |
| 1 |
| 4 |
所以:
| |PA|2+|PB|2 |
| |PC|2 |
| ||
|
故选D
点评:本题给出直角三角形ABC斜边AB上中线AD的中点P,求P到A、B距离的平方和与PC平方的比值,着重考查了用解析法解决平面几何问题的知识点,属于中档题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
 (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=